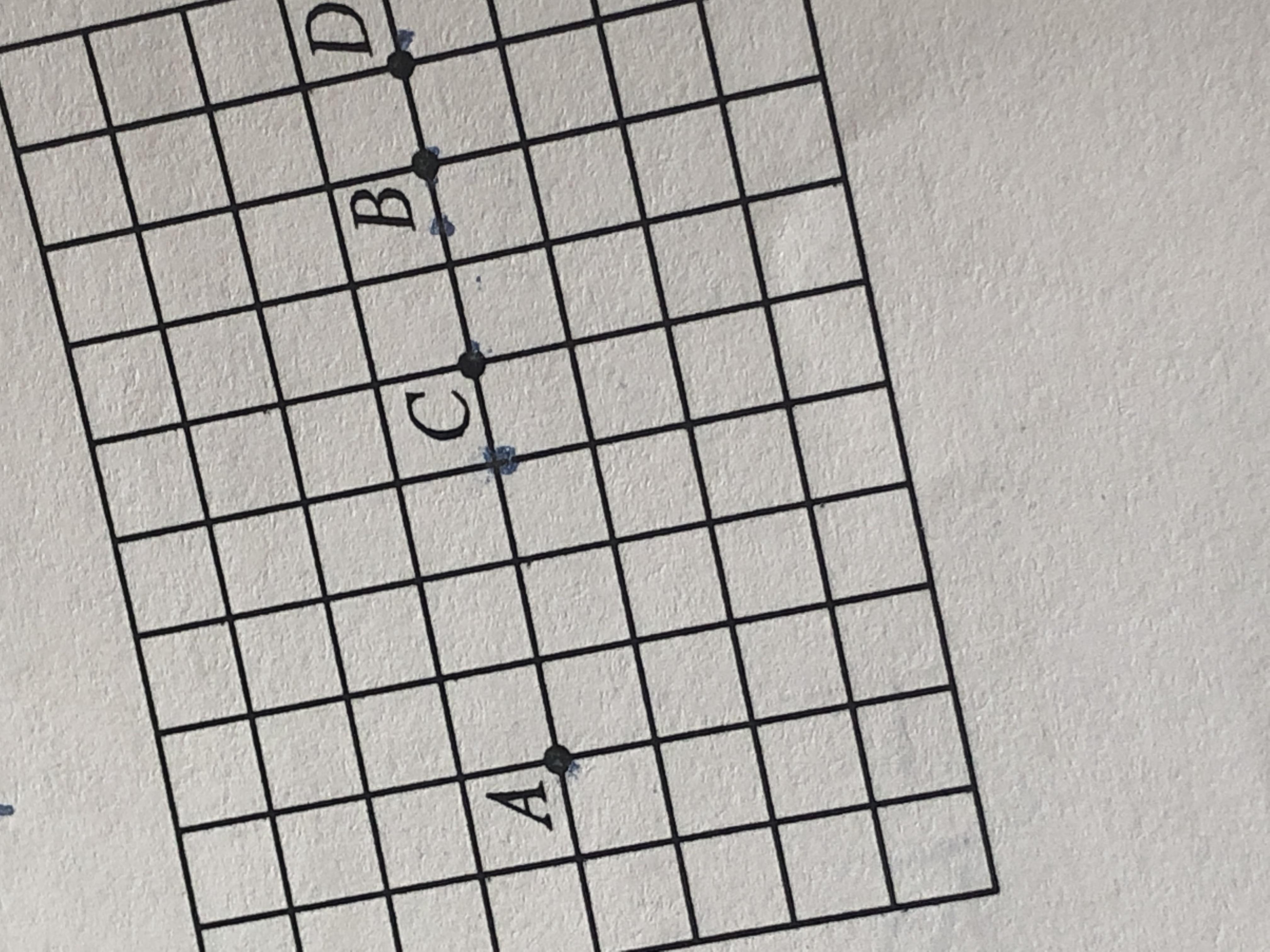
на клетчатой бумаге размером клетки 1х1 отмечены точки A, B, C и D. Найдите расстояние между серединами отрезков AB и CD
Приложения:
Ответы
Ответ дал:
3
Ответ:
расстояние между серединами отрезков AB и CD равно 2.5
Пошаговое объяснение:
определение:
- координата P середины отрезка MN на числовом луче равна полусумме координат концов отрезка взятой по модулю, отсчитывая от точки М.
Пусть точка А имеет координату 0,
тогда
В(6)
С(4)
D(7)
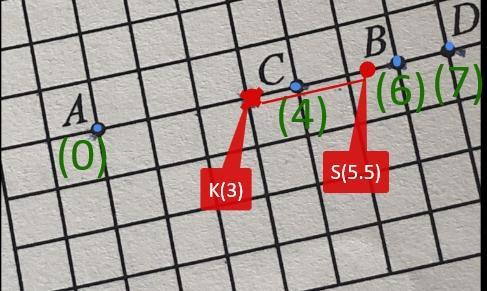
Координата середины отрезка АВ (точка К) отсчитывая от точки А
Координата середины отрезкаCD (точка S) отсчитывая от точки А
Нанесем эти точки на чертеж.
определение:
- расстояние между точками на числовом луче равно разнице их координат, взятой по модулю. .
Расстояние между серединами отрезков АВ и СD равно |SK|
|SK = |5.5 - 3| = 2.5
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад