Question

Найдите радиус окружности, описаного вокруг равнобедреной трапеции, основания который равны 11 и 21 см, а боковая сторона 13 см

Answer 1

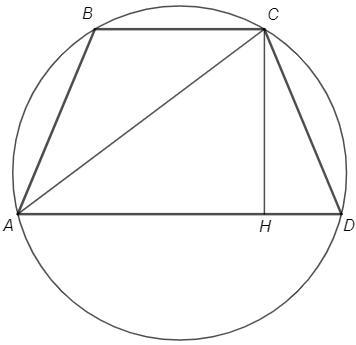
Опустим высоту CH

В равнобедренной трапеции она разделит основание на отрезки, равные полусумме и полуразности оснований.

AH=16, HD=5

CH =√(CD^2 -HD^2) =12 (т Пифагора)

tg(CAH) =CH/AH =12/16 =3/4 => sin(CAH) =3/5 (△CAH - египетский)

CD/sin(CAD) =2R (т синусов) => R =13*5/2*3 =65/6 (см)