СРОЧНО ДАЮ 100 БАЛЛОВ
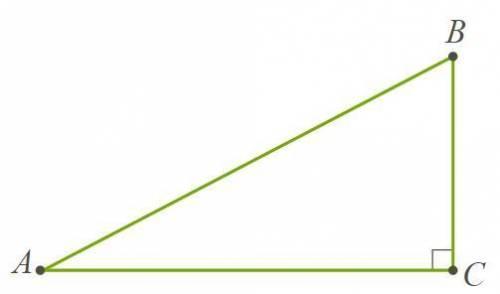
Дан треугольник ABC, у которого ∠C=90°.
Известно, что ctg∠B= 7/24.
Найди AB, если AC=216
Приложения:
orjabinina:
ctg∠B= 7/24 , значит на сторону АС приходится 24 части . И если одна часть х , то 24х=216 , х=9. Тогда сторона ВС=9*7=63. По т. Пифагоа АВ=.........225
CtgB = BC/AC. Значит ВС = 24•216/7.
Ответы
Ответ дал:
1
По т Пифагора:
Ответ: АВ = 225.
CtgB = BC/AC.
ааааа...
(β) = ctgB
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад