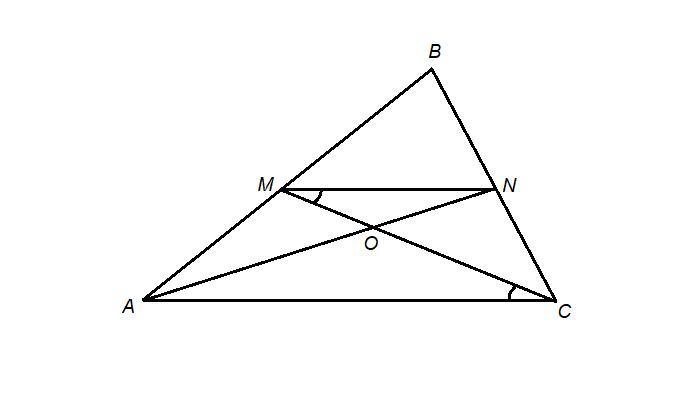
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=30, CM=9. Найдите AO.
Ответы
Ответ дал:
3
Ответ:
20
Объяснение:
Свойство средней линии треугольника:
- средняя линия треугольника параллельна основанию и равна его половине.
MN - средняя линия ΔАВС, значит
MN║AC и MN = 0,5 AC.
ΔMON ~ ΔCOA по двум углам:
∠OMN = ∠OCA как накрест лежащие при пересечении параллельных прямых MN и АС секущей CМ,
углы при вершине О равны как вертикальные.
Пусть AO = x, тогда ON = 30 - x,
x = 2(30 - x)
x = 60 - 2x
3x = 60
x = 20
AO = 20.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад