Ответы
Ответ дал:
2
Розв'язання завдання додаю
Приложения:
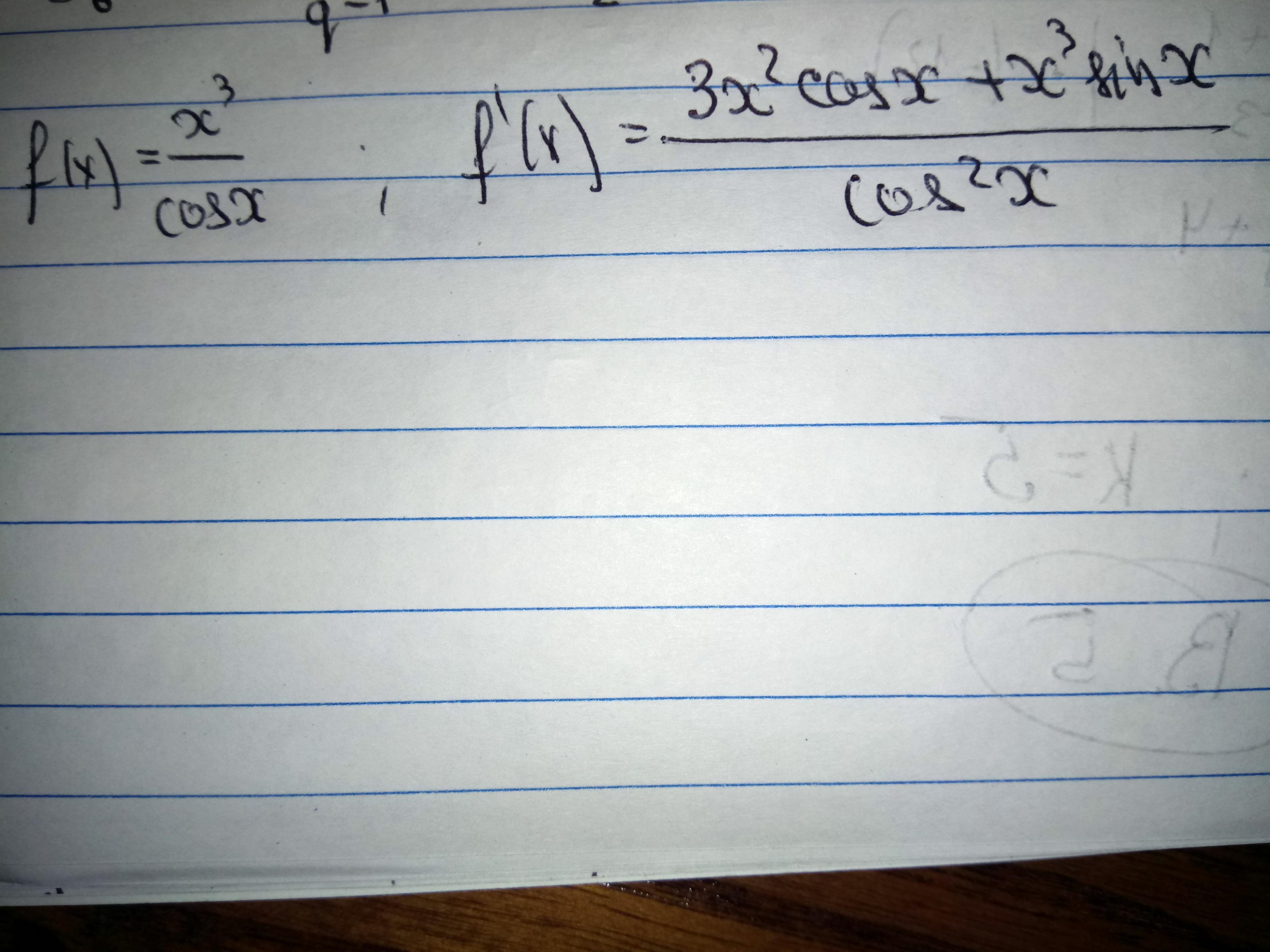
devochka783:
Допоможіть, будь ласка, виконати завдання з алгебри
Ответ дал:
2
Объяснение:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад