Как решить данное дифференциальное уравнение?
Я так полагаю, это диф. уравнение второго порядка без искомого y, допускающее понижение порядка? Пытался решить заменой y" на p*p' и y' на p - не выходит.
Помогите, пожалуйста.
Приложения:
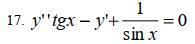
Miroslava227:
здесь нужно брать не p(y), а p(x)
y'=p(x)
y''=p'(x)
и дальше как линейное ДУ
потом к замене возращаетесь
у меня получилось u'*sin(x)=-(1/sin(x)), то есть уже что-то не так, ибо конечный ответ на будет совпадать с ответом от тех же калькуляторов онлайн
Ответы
Ответ дал:
1
Ответ:
Замена:
общее решение
Огромнейшее спасибо!3
:)
помогите мне еще раз , зайдите в вопросах иам есть вопрос без ответа
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад