Определите вид четырехугольника, если его вершины имеют коор-
динаты:
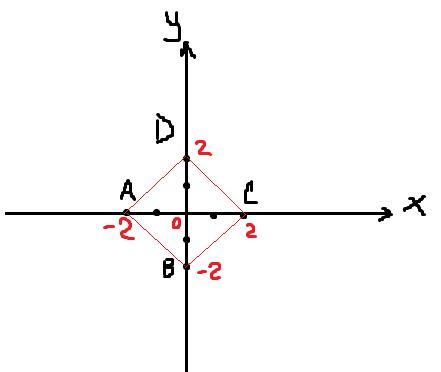
а) А(-2; 0), B(0; -2), С(2; 0), D(0; 2);
Ответы
Ответ дал:
2
Ответ:
квадрат
Объяснение:
Приложения:
orjabinina:
а вдруг углы не 90? А , например, 88 градусов? На глазок этого не видно.
у квадрата есть и другие свойства. равенство диагоналей, например, не оспорить в данном случае
или у прямоугольника.
верно. тогда докажем, что наша фигура - прямоугольник, у которого все стороны равны
(1. равенство сторон) рассмотрим четыре образовавшихся треугольника в прямоугольной системе координат. две стороны каждого равны двум сторонам другого, а угол каждого между этими сторонами равен 90°, т.к. эти углы образуются пересечением осей Х и Y. имеем четыре равных треугольника (по первому признаку равенства треугольников), из чего следует равенство сторон нашей фигуры
(2. прямоугольник) рассмотрим четыре образовавшихся равнобедренных треугольника, углы между боковыми сторонами которых равны 90° (из п.1). найдём углы, прилежащие к основаниям: (180° - 90°)/2 = 45° (по свойствам равнобедренного треугольника). теперь найдём углы нашей фигуры, каждый из которых будет равен: 45°+45° = 90°. следовательно, все углы нашей фигуры прямые
Вывод из п.1 и п.2: искомая фигура является прямоугольником, у которого все стороны равны, что соответствует определению квадрата
длинным путём пошли, конечно, однако получилось нагляднее, на мой взгляд. достаточно сказать, что диагонали перпендикулярны, равны и, пересекаясь, делятся пополам (необходимое и достаточное условие, чтобы фигура являлась квадратом), если потребуется
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад