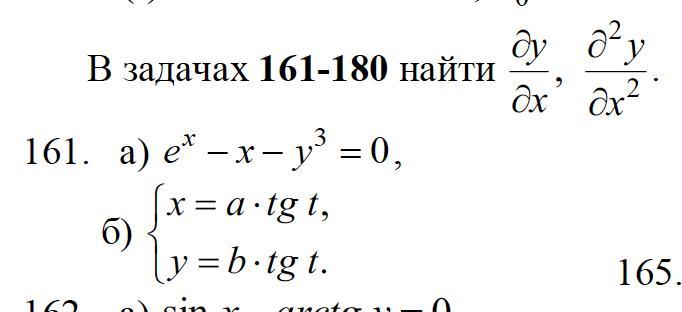Ответы
Ответ дал:
1
Ответ:
a)
_______________________
b)
pushpull:
там в первом случае еще вторая производная по х нужна....
да, сейчас
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад