Ответы
Ответ дал:
1
Ответ:
Это на 100 процентов правильно, мне токоеже задавали и я получила 5 ♡
Приложения:
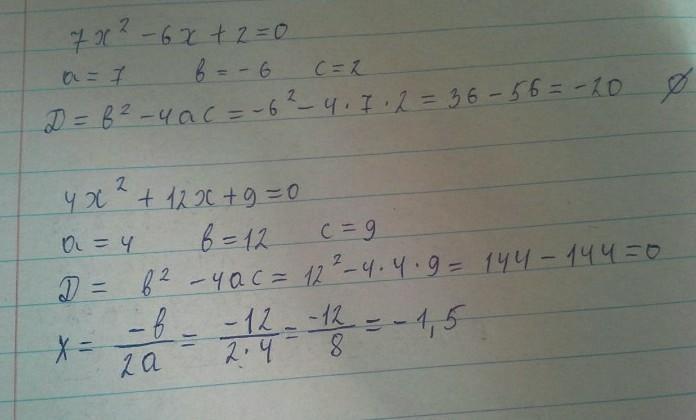
Ответ дал:
1
Объяснение:
Первое уравнение
Второе уравнение корней не имеет
D = b² - 4ac = (-6)² - 4•7•2 = 36-56 = - 20
Третье уравнение:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад