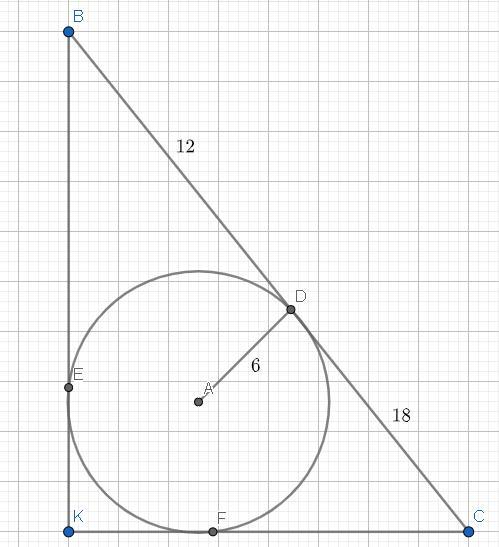
Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 12 см и 18 см. Найти катеты прямоугольника и периметр, если радиус вписанной окружности равен 6 см.
Помогите пожалуйста!!
Ответы
Ответ дал:
1
Я опробовала много способов решения задачи — зная радиус, но в конце концов сделала вывод, что он нам совсем не нужен.
Нам достаточно знать всего лишь отрезки, полученные делением точки касания на гипотенузе.
Теорема о касательных такова: 2 касательные, проведённые с одной точки, в точках касания — равны друг другу.
То есть: BE == BD = 12 (так как оба отрезка проведены с общей точки B).
И ещё: FC == DC = 18 (то же определение).
И также: KE == KF (оба проведены с одной точки (K)).
По теореме Пифагора, гипотенуза равна:
Найдём Дискриминант:
Следовательно:
Следовательно:
Вывод: KC = 24см; BK = 18см; P = 72см.
Приложения:
Аноним:
И если что-то не понятно, то пожалуйста — осведомите мне об этом прямо здесь, в комментариях, и я вам отвечу в личных сообщениях.
Спасибо!)
:D
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад