Question

ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО!!!

Докажите, что четырёхугольник - ромб, если его вершинами являются середины сторон прямоугольника.

Подробно пожалуйста

Answer 1

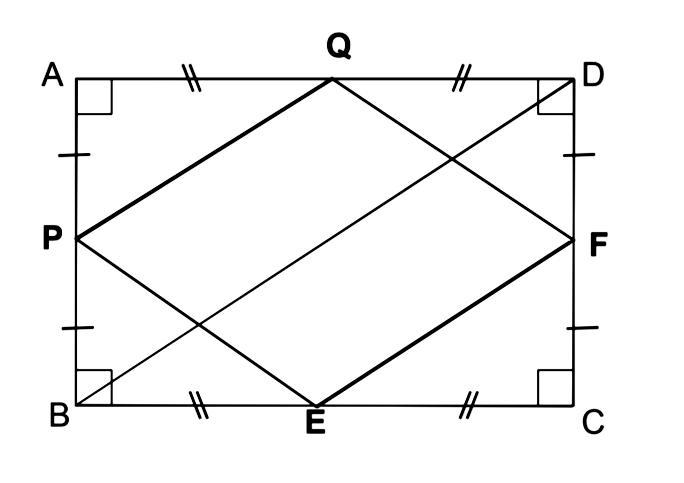
Пусть ABCD - произвольный четырехугольник.

PQ - средняя линия в BAD => PQ||BD, PQ=BD/2

EF - средняя линия в BCD => EF||BD, EF=BD/2

PQ||EF, аналогично PE||QF => PQFE - параллелограмм.

Середины сторон любого четырехугольника являются вершинами параллелограмма (теорема Вариньона).

Стороны параллелограмма Вариньона равны половинам диагоналей четырехугольника.

Диагонали прямоугольника равны => стороны параллелограмма Варионьона равны, он является ромбом.