Question

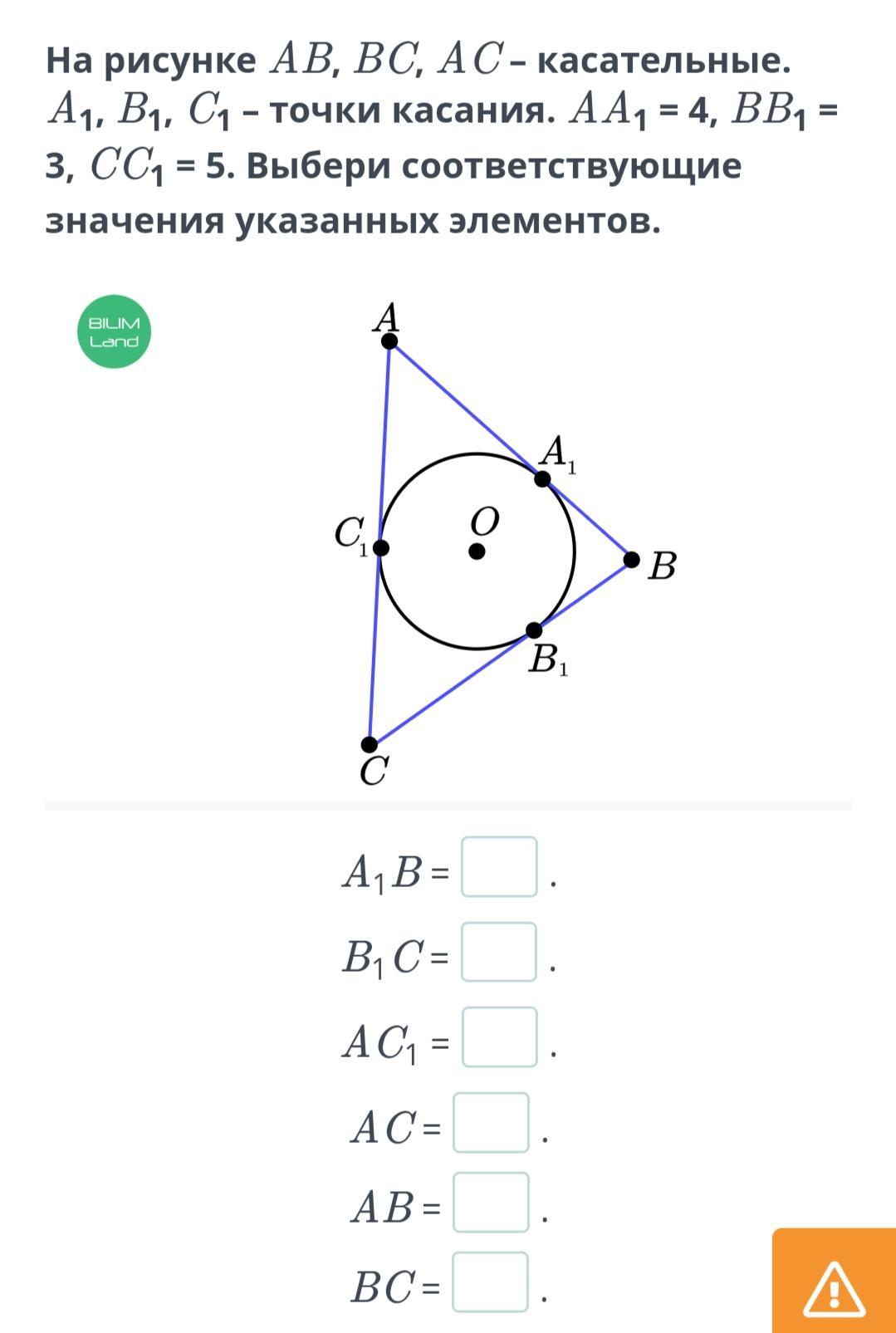
На рисунке AB, BC, AC – касательные. A1, B1, C1 – точки касания. AA1 = 4, BB1 = 3, CC1 = 5. Выбери соответствующие значения указанных элементов.

Answer 1

Ответ:

$\boxed{A_{1}B = 3}$

$\boxed{B_{1}C = 5}$

$\boxed{AC_{1} = 4}$

$\boxed{AC = 9}$

$\boxed{AB = 7}$

$\boxed{BC = 8}$

Объяснение:

Дано: AB, BC, AC – касательные; $A_{1},B_{1},C_{1}$ - точки касания, $AA_{1} = 4$, $BB_{1} = 3$, $CC_{1} = 5$, O - центр окружность

Найти: $A_{1}B,B_{1}C,AC_{1},AC,AB,BC$ - ?

Решение:

Так как по условию AB, BC, AC – касательные; $A_{1},B_{1},C_{1}$ - точки касания, то есть касательные имеют точки пересечения, то окружность с центром O вписана в треугольник ΔABC.

По свойству отрезков касательных, проведенной из одной точки: $\boxed{A_{1}B = B_{1}B = 3, C_{1}C = B_{1}C = 5, C_{1}A = A_{1}A = 4}$

По основному свойству отрезка:

$BC = BB_{1} + CB_{1} = 3 + 5 = 8$

$AB = AA_{1} + BA_{1} = 4 + 3 = 7$

$AC = CC_{1} + AC_{1} = 5 + 4 = 9$

Answer 2

На рисунке AB, BC, AC – касательные. A1, B1, C1 – точки касания. AA1 = 4, BB1 = 3, CC1 = 5. Найти: А₁В, В₁С, АС₁, АС, АВ, ВС

Ответ:

А₁В = 3,

В₁С = 5,

АС₁ = 4,

АС = 9,

АВ = 7,

ВС = 8.

Объяснение:

Дано: AB, BC, AC – касательные к окружности с центром в т.О.

A₁, B₁, C₁ – точки касания. AA₁ = 4, BB₁ = 3, CC₁ = 5.

Найти: А₁В, В₁С, АС₁, АС, АВ, ВС

• Отрезки касательных к окружности, проведенных из одной точки равны.

1) А₁В = BB₁ = 3, так как А₁В и BB₁ - касательные к окружности, проведенные из одной точки В.

2) В₁С = CC₁ = 5, так как В₁С и CC₁ - касательные к окружности, проведенные из одной точки С.

3) АС₁ = AA₁ = 4, так как АС₁ и AA₁ - касательные к окружности, проведенные из одной точки А.

• Если нa отрезке поставить точку, то она разделит его на два отрезка, сумма длин которых равна длине исходного отрезка

Следовательно:

4) АС = АС₁ +  CC₁ = 4 + 5 = 9

5) АВ = AA₁ + А₁В = 4 + 3 = 7

6) ВС = BB₁ + В₁С = 3 + 5 = 8