Срочноооооооооо ребятааааа помогитеее с полным решением (не обведено
Приложения:
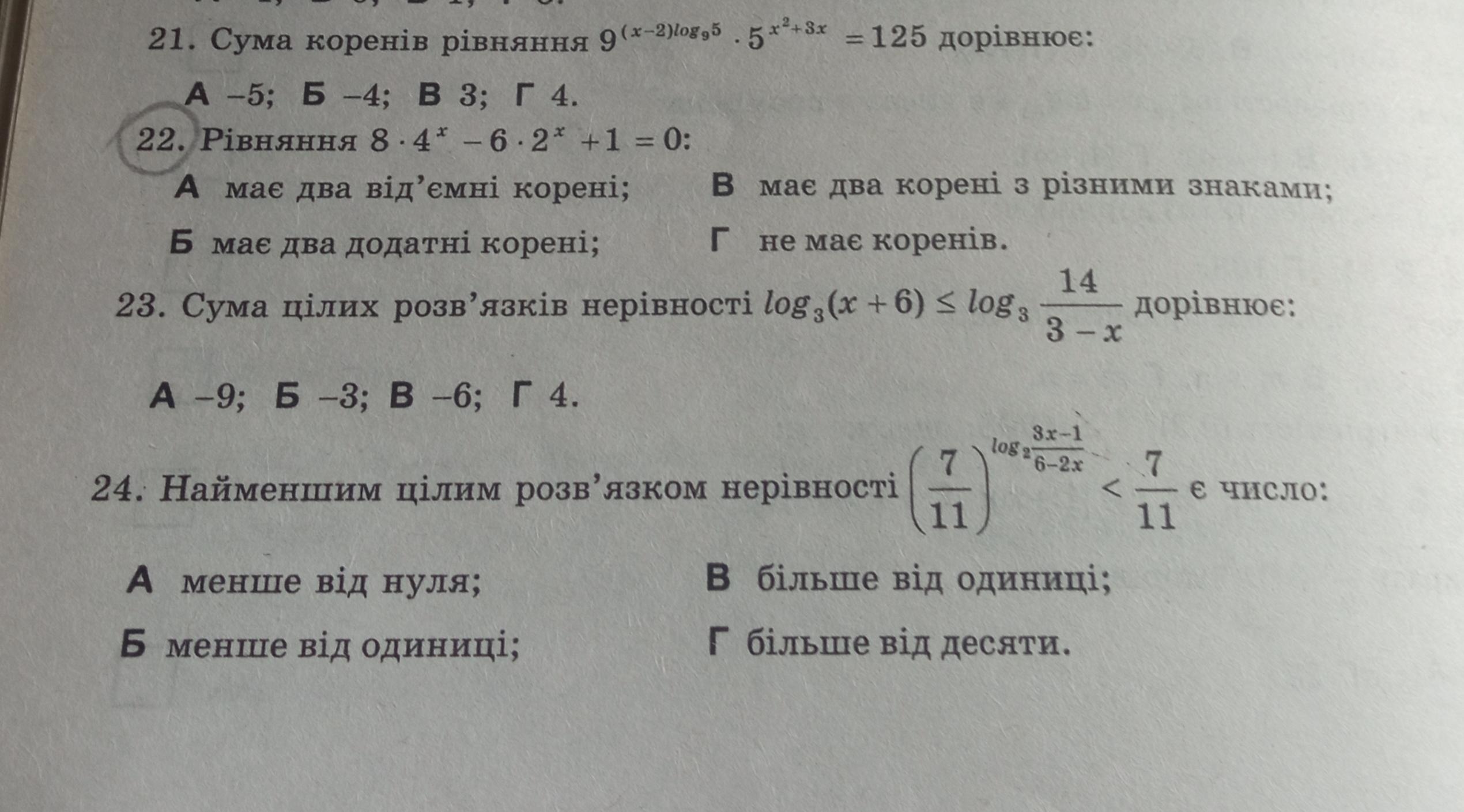
nightcore52:
по русски можно?
Ответы
Ответ дал:
0
1.
Вiдповiдь: - 4
2.
1)
2)
Вiдповiдь: А)
3.
=>
(
)
" _" "+" " _"
______-6________-4__________1________3_________
Вiдповiдь: B) - 6
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад