Ответы
Ответ дал:
2
Ответ:
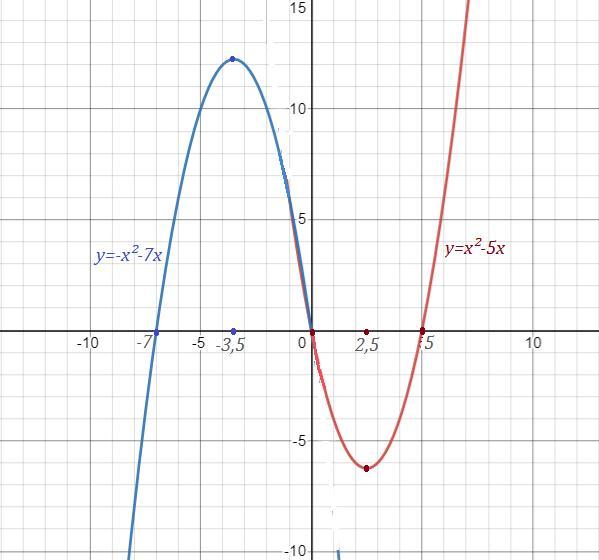
Строим параболу у=х²-5х на промежутке х∈[ 0 ;+∞ ) . Ветви параболы направлены вверх, вершина в точке (2,5 ; -6,25) . Точки пересечения с ОХ: (0;0) и (5;0) .
Параболу у=-х²-7х строим на промежутке х∈( -∞ ; 0 ] . Ветви параболы направлены вниз, вершина в точке (-3,5 ; 12,25) . Точки пересечения с ОХ: (0;0) и (-7;0) .
График нарисован сплошными линиями .
Прямая у=m имеет с заданным графиком ровно 2 общие точки при
m= -6,25 и при m=12,25 .
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад