Найдите площадь фигуры, ограниченную параболой  , касательной, проведённой к данной параболе в точке с абциссой
, касательной, проведённой к данной параболе в точке с абциссой  , и осью ординат.
, и осью ординат.
Ответы
Ответ дал:
1
Ответ:
- уравнение касательной
_______________
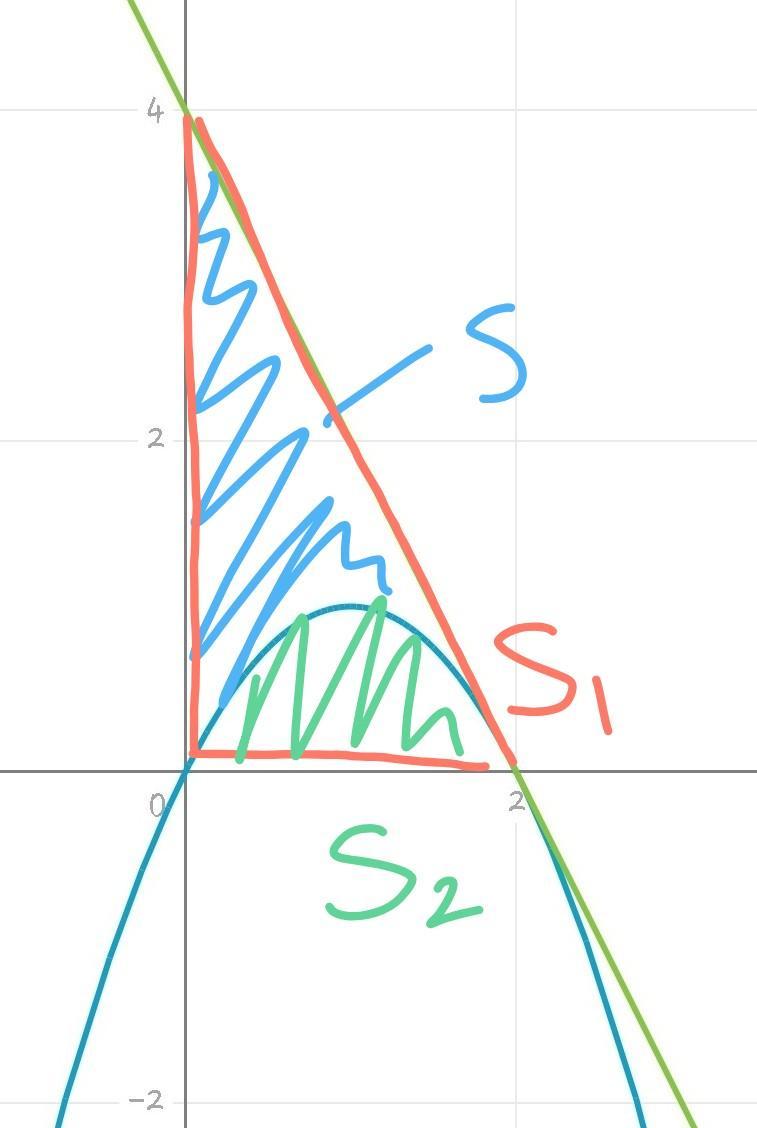
рисунок
Ответ: 8/3
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад