Вычислить площадь фигуры, ограниченной заданными линиями.
Выполнить рисунки.
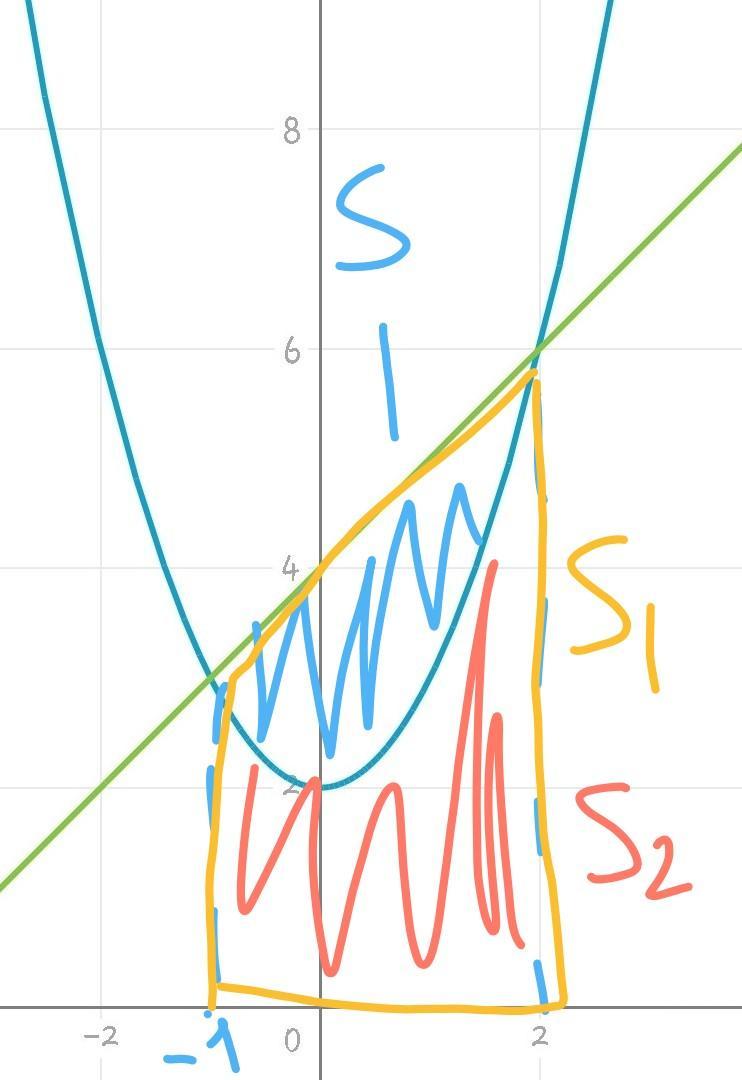
1)y=x^2+2, y=x+4
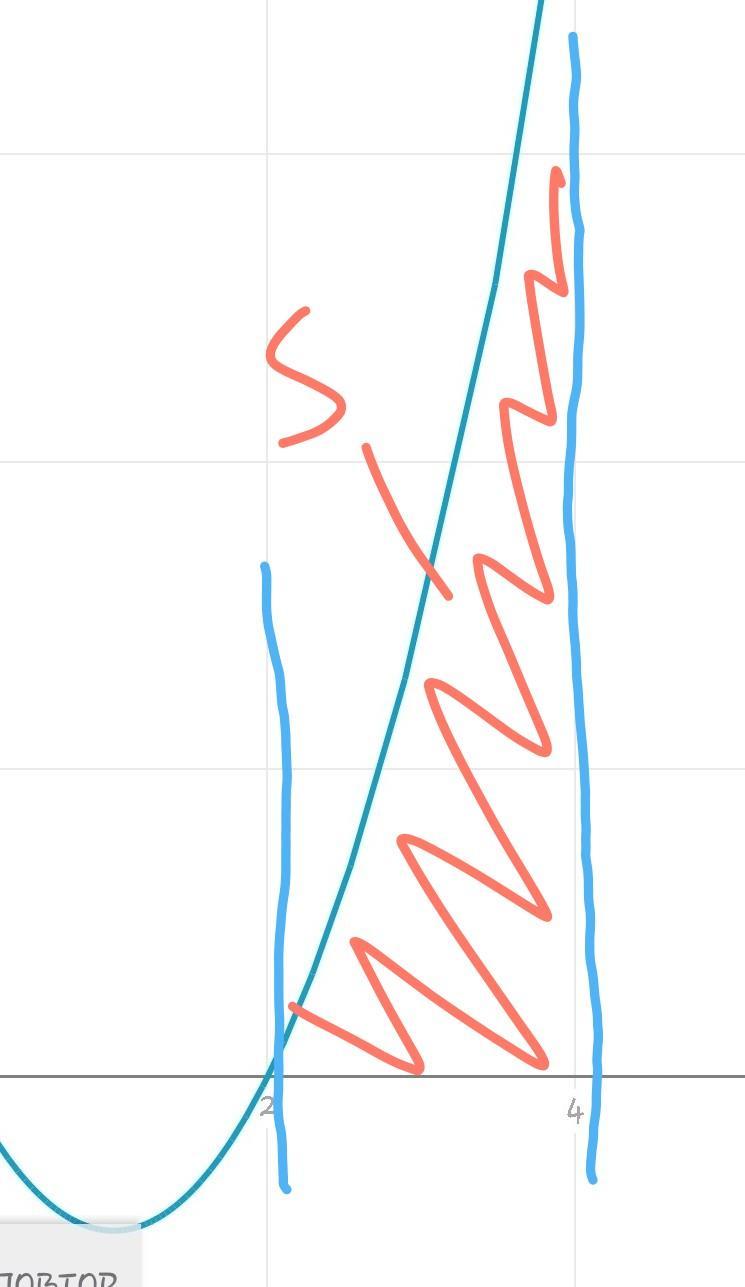
2)y=x^2-2x, x=2, X=4, y=0
Даю 100 балов, заранее спасибо.
Ответы
Ответ дал:
2
Ответ:
1.
рисунок1
2.
рисунок2
Приложения:
срочно
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
1. Бумалардың жалпыға қолжетімді болуы пайдаланушы үшін
қаншалық маңызы бар?
2. Жалпыға қолжетімді бумалармен жұмыс істеудің қандай тиімді
және тиімсіз жақтары бар?
3. Жалпыға қолжетімді бумалар компьютерде қандай тапсыр-
маларды орындағанда қолайлы?
СРОЧНО маған көмектесшиндерши