Question

Помогите пожалуйста с решением. Подробно всё распишите.

Answer 1

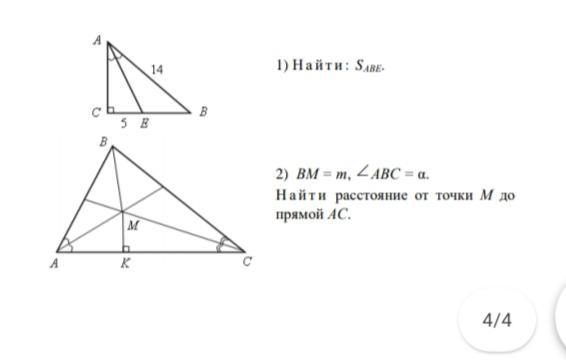
1) Будем считать, что задано условия: АЕ - биссектриса угла А, СЕ = 5, АВ = 14.

Пусть координаты точек: В(x; 0), A(0; y).

Используем свойство биссектрисы: 5/у = (х - 5)/14, отсюда ху - 5у = 70.

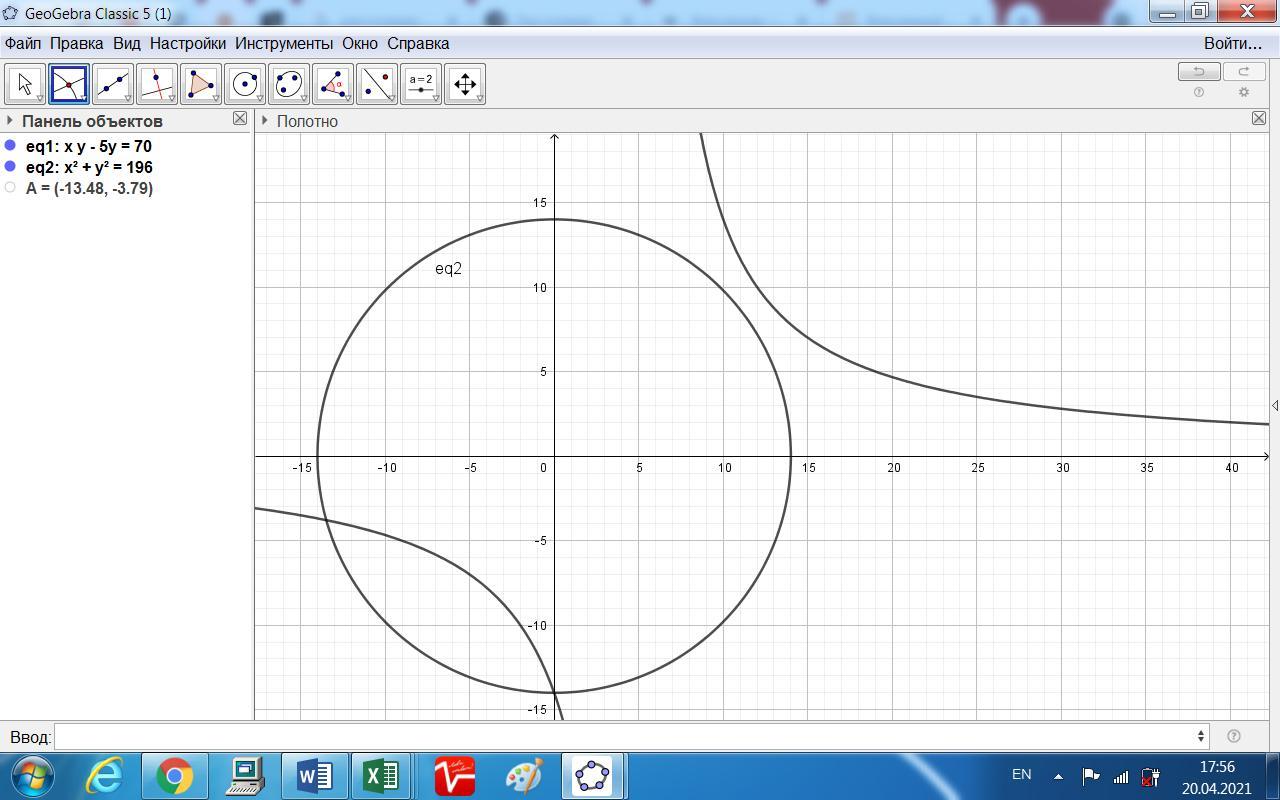
Или у = 70/(х - 5). Это уравнение гиперболы.

По Пифагору х² + у² = 14². Это уравнение окружности.

Решить систему можно графически.

Во вложении дан график этих функций.

Как видим, решения нет, только в области отрицательных значений есть точки пересечения, но к решению их нельзя отнести.

2) Здесь надо применить формулу.

r = BM*sin(B/2), где угол В - это угол АВС, а расстояние r от точки М до прямой АС - это радиус вписанной окружности.