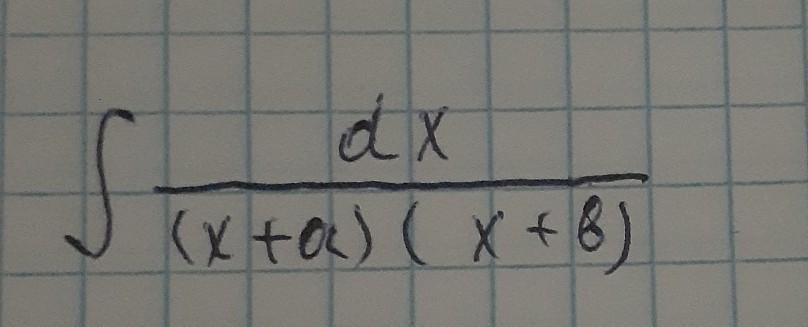Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
здесь самое важное разложить дробь на слагаемые. а потом уже как по накатанному
теперь будем делать замену переменных в каждом интеграле
теперь подставим обратные замены, произведем преобразования и получим
AsliddinFML:
Вы можете написать мне телеграммой? Мне снова нужна твоя помощь Мой профиль в Telegram: @AsliddinTDTU
ну, я вроде как подключилась....
Вы можете написать мне телеграммой? Мне снова нужно твоя помощь Мой профиль в Telegram: @AsliddinTDTU
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад