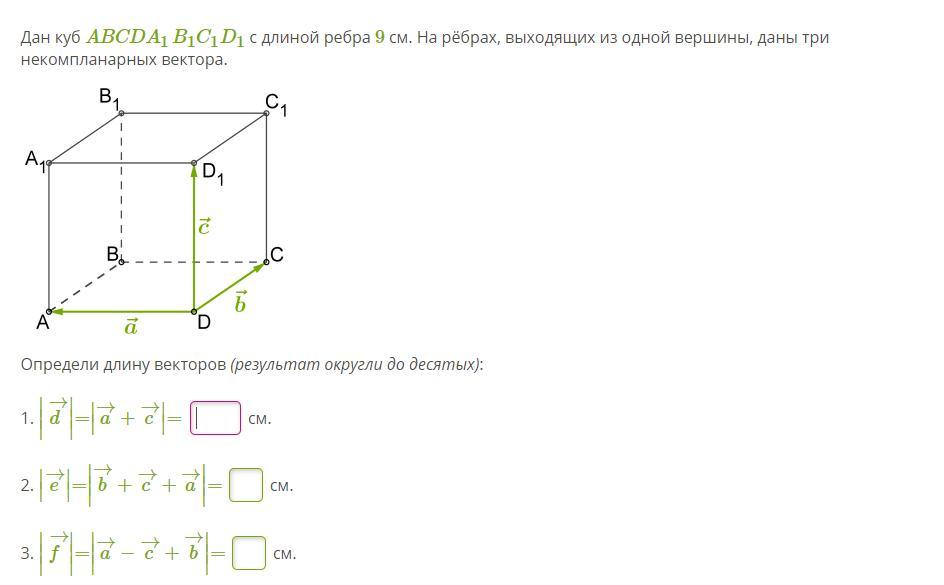
Дан куб ABCDA1B1C1D1 с длиной ребра 9 см. На рёбрах, выходящих из одной вершины, даны три некомпланарных вектора.
Приложения:
Ответы
Ответ дал:
1
|a+c| складывается по правилу треугольника. |d| =
=12.7
для вектора е соединяешь вектора b, c и а так, чтобы из конца одного выходило начало другого (как у треугольника). выходит, что вектор е=диагонали В1D, т.е.
=15.5
вектор f=а+(-с)+b, т.е. сейчас вектор с направлен вверх, а -с будет направлен вниз. так же по правилу многоугольника складываем, получая, что f=BD1. это куб, поэтому диагонали равны. f=15.5
d=12.7; e=f=15.5
PomogitiPozhalujsto:
e и f равны 15.6
не в ту сторону округлил, извиняюсь
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад