Question

помогите пожалуйста!!!

Answer 1

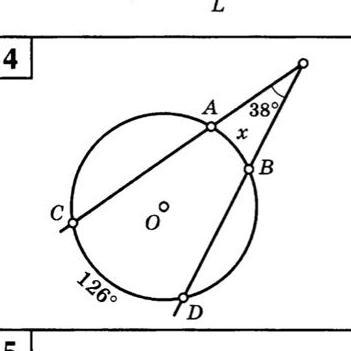
На рисунке  4 две секущие  окружности пересекаются под углом 38°. Нужно найти градусную меру меньшей дуги  х между ними, если большая равна 126°

Ответ: 50°

Объяснение:

Пусть М - точка пересечения секущих СА и DB.

Решение:

Способ 1)

Угол между двумя секущими (с вершиной вне окружности) равен полуразности дуг, высекаемых секущими на окружности . =>

(◡СD- ◡AB):2=38°

(◡СD- ◡AB)=2•38°=76° =>

◡AB=◡СD-76°=126°-76°=50°

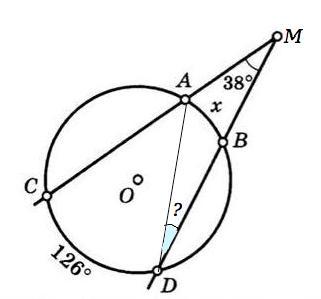
Способ 2)

 Вписанный угол равен половине градусной меры дуги, на которую он опирается. =>

∠САD=126°:2=63°

∠САМ- развернутый и равен 180°.

∠МАD=180°-63°=117°

Из суммы углов треугольника в ∆ МАD ∠D=180°-117°-38°=25°

∠ АDМ - вписанный, поэтому дуга АВ вдвое больше его градусной меры.

◡AB=2•25°=50°