Рациональное неравенство. Урок 4
2
—
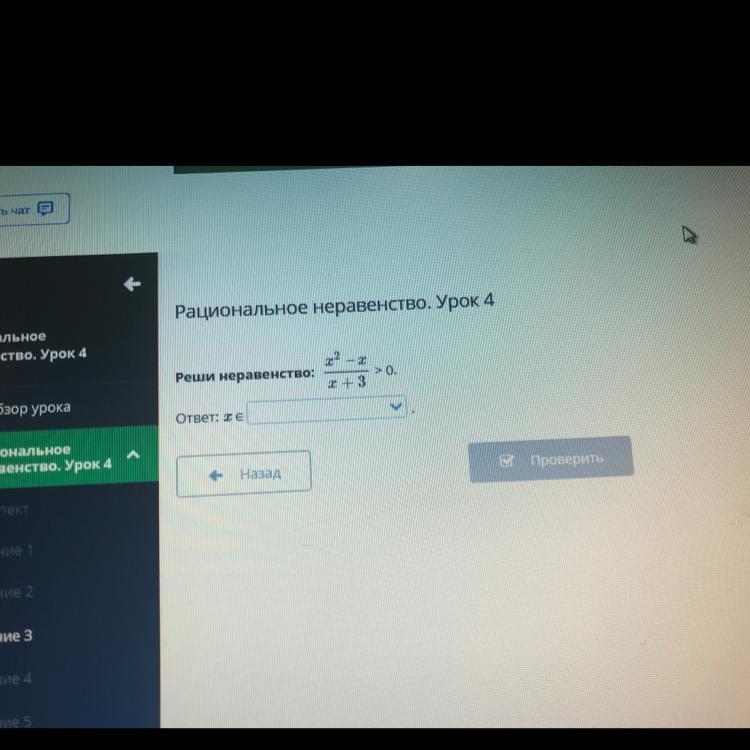
Реши неравенство:
> 0.
I + 3
Ответ: ТЕ
к4 л
е
Назад
0 Проверить
Приложения:
aruzankajrzankyzy:
Я думаю что ответ есть ?
Ответы
Ответ дал:
2
Ответ:
x ∈ (-3; 0) ∪(1; +∞)
Объяснение:
Рассмотрим функцию
Область определения функции - все числа, кроме - 3.
Так как делить на нуль нельзя.
- нули функции.
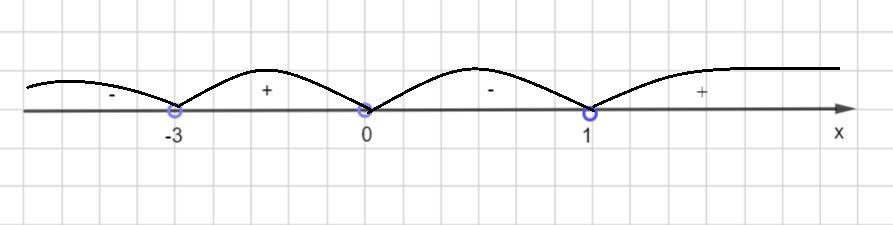
Определим знак функции на каждом промежутке и получим:
x ∈ (-3; 0) ∪(1; +∞)
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад