Question

Сделать описание чертежа и доказать, что АО=Со. Задание на фото.

Answer 1

Объяснение:

Дано:

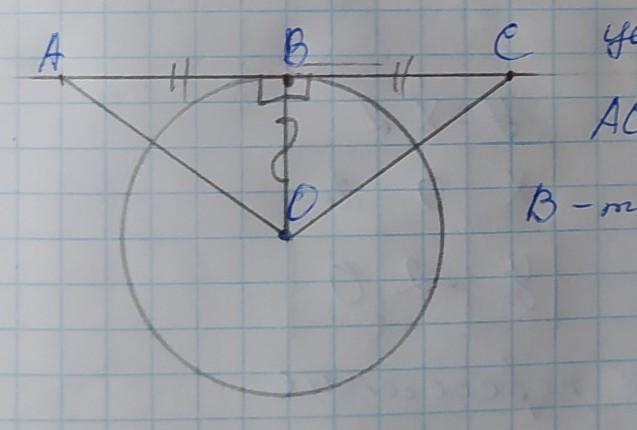
окружность с центром в точке О;

АС - касательная;

В - точка касания

АВ=ВС

Доказать: АО=СО

=============================

ДОКАЗАТЕЛЬСТВО:

Проведём радиус ОВ. Радиус с точкой касания образуют прямой угол =90°. ВО делит ∆АОС на 2 прямоугольных треугольника АОВ и СОВ. Рассмотрим эти треугольники:

У них:

1) АВ=ВС - по условию

2) ВО - общая сторона

3) уголАВО=уголСВО=90°

Следовательно эти треугольники равны по первому признаку: по двум сторонам и углу между ними, (∆АОВ=∆СОВ), значит АО=СО

ДОКАЗАНО