Question

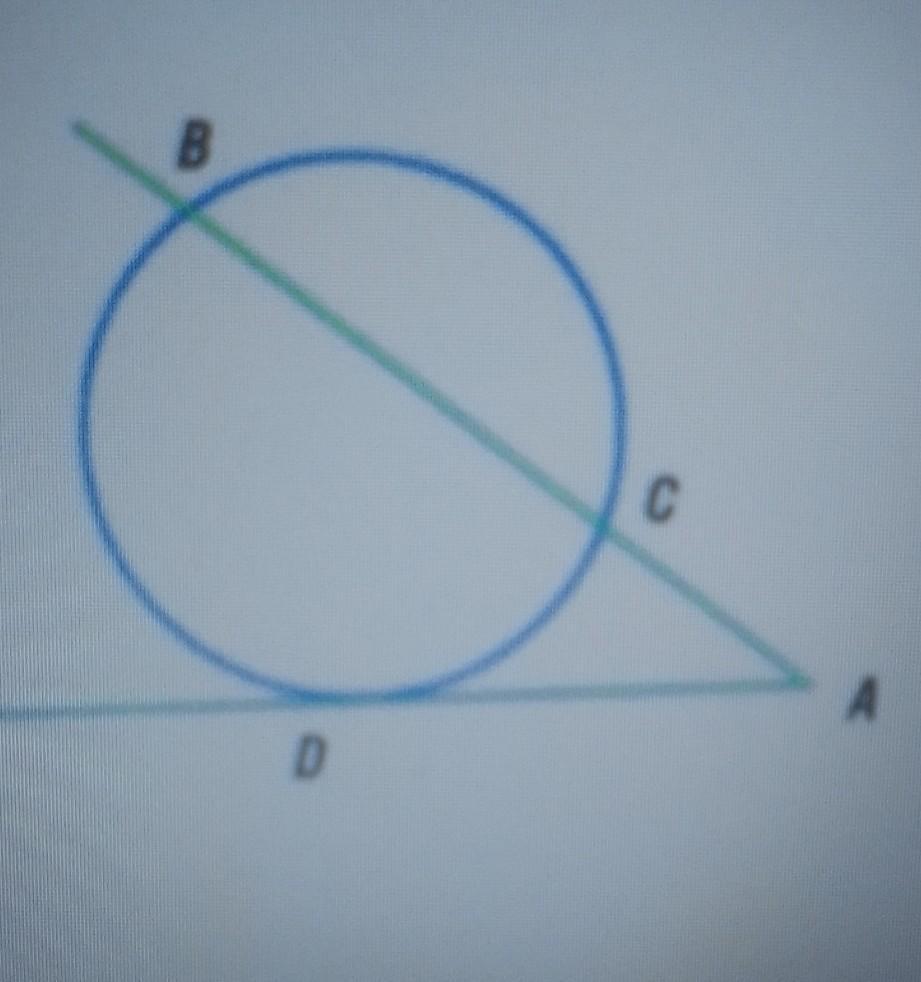
Из точки А проведены секущая AB = 16 и касательная AD к окружности.
Найди AD, если известно, что АС на 3 меньше, чем AD, а искомая
касательная AD больше 5.​

Answer 1

Ответ:12

Пошаговое объяснение:

Для касательной и секущей к окружности, проведённых из одной точки, квадрат расстояния от этой точки до точки касания равен произведению длины секущей на длину её внешней части.

То есть, AD²=AB*AC

Пусть AD=x, тогда АС=x-3

Составим уравнение:

x²=16*(x-3)

x²-16x+48=0  (раскрыл скобки и перенёс правую часть влево)

по теореме Виета:

x1+x2=16

x1*x2=48

получим корни  

x1=4 , x2=12

по условию задачи подходит корень 12

Ответ:12