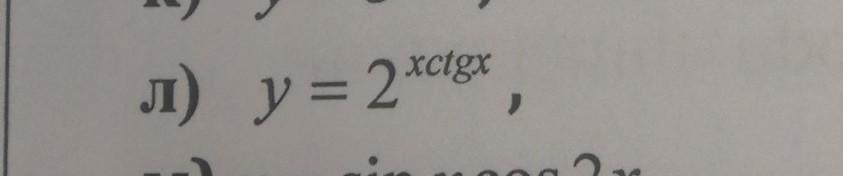Ответы
Ответ дал:
1
Мы имеем дело с производной сложной функции: у' = (2^(x·ctgx))' = 2^(x·ctgx) · ㏑2 · (x·ctgx)' = 2^(x·ctgx) · ㏑2 · (1·ctgx + x · (-1/sin²x)) =
2^(x·ctgx) · (ctgx - x/sin²x) · ㏑2
б) пусть у = 3^(-x²), тогда y' = 3^(-x²) · ㏑3 · (-2x)
amanda2sempl:
пусть у = 3^(-x²), тогда y' = 3^(-x²) · ㏑3 · (-2x)
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад