Question

АЛГЕБРА! Задача! Люди добрі, ДОПОМОЖІТЬ будь ласка, дуже сильно прошу Вас(((​

Answer 1

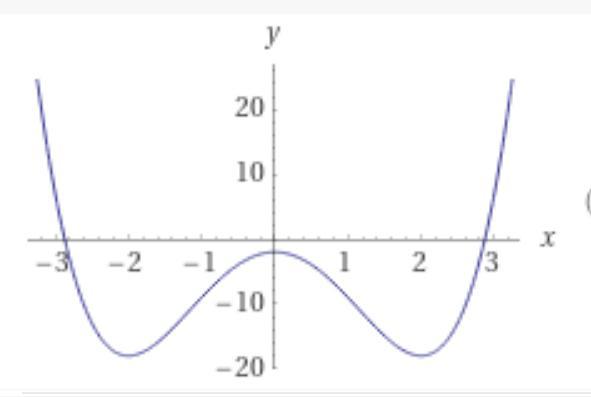
Дана биквадратная функция y = x^4 - 8x^2 - 2.

Её производная равна: y' = 4x^3 - 16x = 4x(x^2 - 4).

Приравняем её нулю: 4x(x^2 - 4) = 0, x1 = 0.

x2.3 = √4 = ±2, x2 = 2, x3 = -2.

Это точки экстремумов. Находим их свойства, определив знаки производной.

х =  -3     -2    -1      0    1      2       3

y' = -60    0     12    0    -12    0     60.

Как видим, в точках х = -2 и х = 2 минимум функции (y' от- к +).

в точке х = 0 - максимум (y' от + к -).

Подставим найденные критические точки в уравнение и определяем:

максимум функции у(мах) = -2 при х = 0,

минимум функции у(мин) = -18 при х = -2 и х = 2.

На заданном промежутке минимум у = -18 в точке х = 2, а максимум в точке х = 3. Значение у = 3^4 - 8*3^2 - 2 = 81 - 72 - 2 = 7.