Найдите точку минимума у функции. Почему у меня получается ответ, будто у этой функции нет минимума?
Приложения:
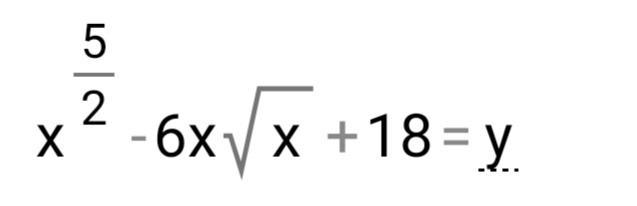
Ответы
Ответ дал:
1
Дана функция y = x^(5/2) - 6x^(3/2) + 18.
Так как степени нечётные, то у функции отсутствуют отрицательные значения переменной х.
Находим её производную:
y' = (5/2)*x^(3/2) - (18/2)*x^(1/2) = (1/2)√x*(5x-18).
Для нахождения экстремумов приравниваем производную нулю.
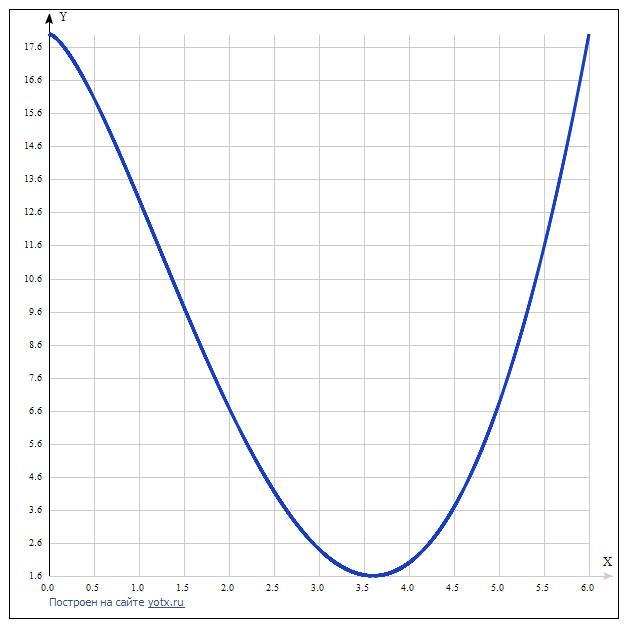
Имеем 2 значения: х = 0 и х = 18/5 = 3,6.
Находим значения переменной левее и правее критических точек.
х = 0 1 18/5 4
y' = 0 -6,5 0 2.
Как видим, функция имеет минимум в точке х = 18/5, так как производная меняет знак с минуса на плюс.
Значение функции в этой точке у = 1,60675261.
.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад