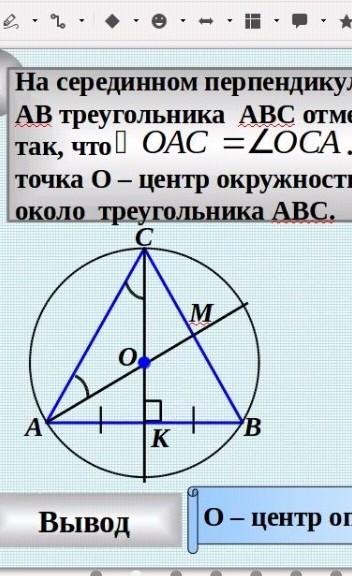
Помогите пожалуйста!!!На серединном перпендикуляре стороны АВ треугольника АВС отмечена точка О та что ОАС равен ОСА. Докажите что точка О центр окружности описанной около треугольника АВС
Приложения:
Ответы
Ответ дал:
0
Ответ :
т.О — центр описанной около ∆ АВС окружности, ч.т.д.
Объяснение:
В ∆ АОС углы при основании АС равны. Следовательно, ∆ АОС –равнобедренный, и АО=ОС.
В ∆ АОВ отрезок ОМ⊥АВ и делит её пополам. ⇒
ОМ высота и медиана ∆ АОВ. ⇒ ∆ АОВ — равнобедренный, и
АО=ОВ. Отрезки АО=ОВ=ОС
Точки А, В и С находятся на одном и том же расстоянии от О, следовательно, принадлежат окружности, так как ей принадлежит множество точек плоскости, находящихся на одном и том же расстоянии от одной точки, следовательно
(ответ сверху)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
В ∆ АОВ отрезок ОК⊥АВ и делит её пополам. ⇒
ОК высота и медиана ∆ АОВ. ⇒ ∆ АОВ — равнобедренный, и
АО=ОВ. Отрезки АО=ОВ=ОС .
Точки А, В и С находятся на одном и том же расстоянии от О, следовательно, принадлежат окружности, так как ей принадлежит множество точек плоскости, находящихся на одном и том же расстоянии от одной точки⇒ О-центр описанной окружности