Площа прямокутного трикутника дорівнює 60 см², а один із катетів – 15 см. Знайти радіус кола, описаного навколо трикутника.
нужно через нехай дано
orjabinina:
Площадь прямоугольного треугольника равна 60 см², а один из катетов - 15 см. Найти радиус окружности, описанной около треугольника.
ΔАВС-прямоугольный , ВС=15 см. Значит 60=1/2*15*АС, АС=(60*2):15=8 см.Радиус описанной окружности лежит на середине гипотенузы . Ищем гипотенузу.
Знаешь как?
Знаешь как?
нет
По т. Пифагора. Её -то знаешь?
ааа
точно
и все?
точнее спасибо
Ответы
Ответ дал:
10
Ответ:
8,5 см
Объяснение:
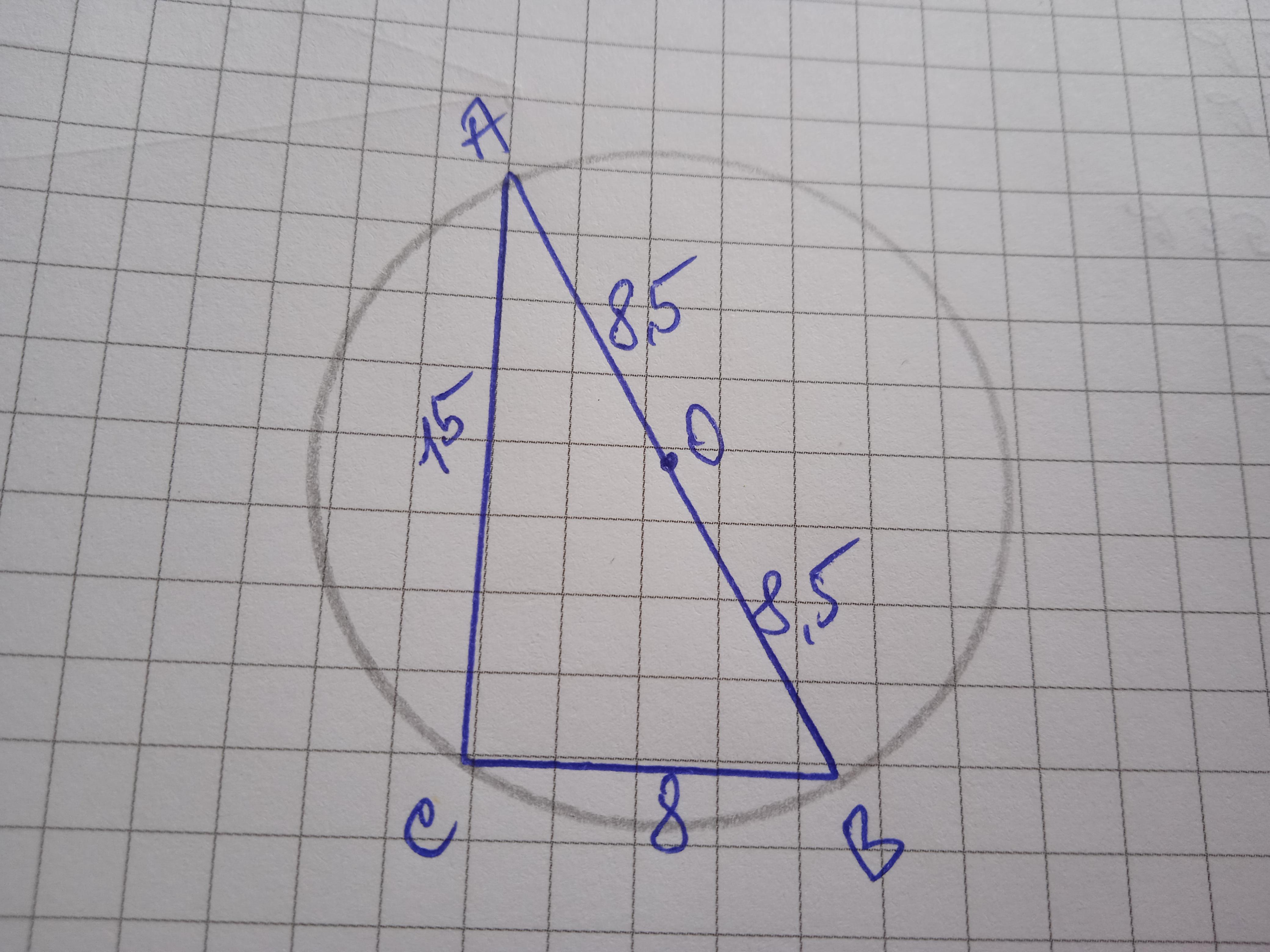
Дано: ΔАВС, ∠С=90°, АС=15 см. Знайти R.
Знайдемо ВС за формулою площі трикутника
60=1/2 * 15 * ВС
ВС=60:7,5=8 см.
Знайдемо АВ за теоремою Піфагора
АВ=√(АС²+ВС²)=√225+64=√289=17 см
Центром описаного кола є точка середини гіпотенузи, отже
R=17:2=8,5 см
Приложения:
эх
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад