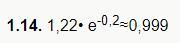Ответы
Ответ дал:
0
Пусть случайная величина Х-это количество отказов элементов, которое может принимать значения 0;1;2;3;...100.
Вероятности этих значений найдем по формуле Пуассона, т.к. n=100, р=0.02- малая вероятность.
λ=100*0.002=0.2
Р(Х=к)=(λ^(к))*е^(-λ)/к!
λ=nр-среднее число появления событий в n независимых испытаниях.
Р(Х=0)=(0.2⁰))*е⁻⁰.²/0!=е⁻²
Р(Х=1)=(0.2¹))*е⁻⁰.²/1!=0.2е⁻²
Р(Х=2)=(0.2²))*е⁻⁰.²/2!=0.02е⁻²
а искомая вероятность - это вероятность того, что за время Т откажет не более двух элементов- т.е. меньше или два, иными словами, откажут или два, или один, или ни один элемент, равна сумме вероятностей по формуле сложения.
е⁻²+0.2е⁻²+0.02е⁻²=1.22е⁻²
Ответ 1.22е⁻²
Аноним:
Можете написать формулы на листочке я не помойму как записать
Р(Х=к)=(λ^(к))*е^(-λ)/к! -в числителе λ в степени к, умноженная на е в степени λ, в знаменателе к!.
http://prnt.sc/120s9iq так ?
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
9 лет назад