Ответы
Ответ дал:
0
Ответ:
Приложения:
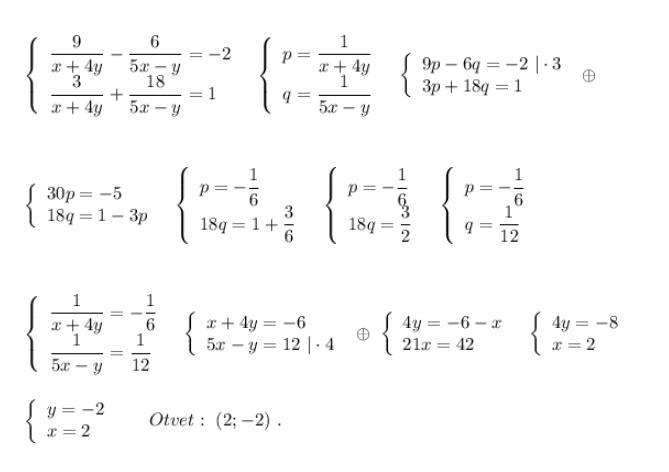
NNNLLL54:
А если тебе не надо писать сначала замену, то чего трудного? Пиши в решении вместо p и q дроби, которые я указала, и всё ! Соображать надо хоть что-нибудь!
нужно отталкиваться от того, как делать более РАЦИОНАЛЬНО !
причём, твой метод сложения ПРИМЕНЁН !
ВМЕСТЕ С ЗАМЕНОЙ!
Идите далеко-далеко раз нормально отвечать на вопросы не умеете.
Ну и что, что с заменой ? В условии не сказано, что не надо метод замены применять ... Всё надо указывать в условии....
Это ты невоспитанное хамло вместо спасибо за решение гадости говоришь, даже не понимая ничего в математике...
Во-первых, вы, а во-вторых, идите уже, "магистр".
Вы говорят воспитанным людям, а тебя родители не умудрились воспитать, наверное сами такие
Взаимно.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад