Question

50баллов геометрия срочно все на скрине​

Answer 1

Ответ:

$\boxed{P_{зABC} = 120}$

Объяснение:

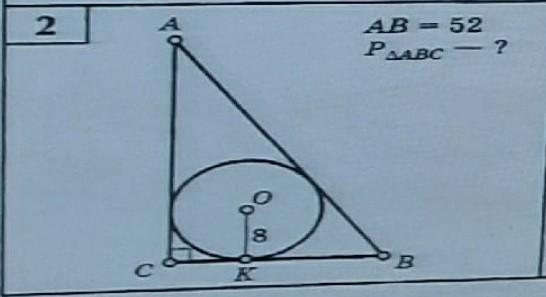
Дано: ∠ACB = 90°, OK - радиус вписанной окружности, AB = 52, OK = 8

Найти: $P_{зABC} \ - \ ?$

Решение:

По формуле радиуса вписанной окружности для прямоугольного

треугольника (по условию угол ∠ACB = 90°):

$OK = \dfrac{AC + BC - AB}{2} \Longrightarrow AC + BC = 2OK + AB = 2 \cdot 8 + 52 = 16 +52 = 68$

По определению периметра треугольника (ΔACB):

$P_{зABC} = AC + BC + AB = 68 + 52 = 120$.