Висота рівнобедреного трикутника, що проведена до його основи, дорівнює 15 см, а бічна сторона відноситься до основи як 2:1. Знайдіть радіус кола, вписаного в трикутник
Ответы
Ответ дал:
4
Высота равнобедренного треугольника, проведенная к его основанию, равна 15 см, а боковая сторона относится к основанию как 2: 1. Найдите радиус окружности, вписанной в треугольник.
—————
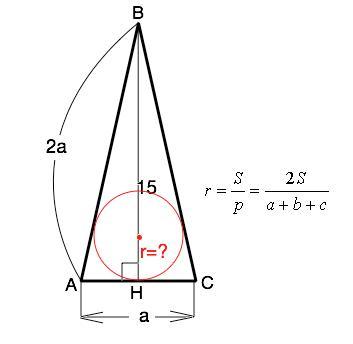
Примем основание АС равнобедренного треугольника АВС равным а, тогда боковые стороны равны по 2а.
Для окружности, вписанной в произвольный треугольник, r=S:p=2S:P, где Ѕ - площадь треугольника, р - его полупериметр, Р - периметр.
Площадь треугольника равна половине произведения высоты на сторону, к которой проведена. =>
2Ѕ=ВН•АС=15•а
Р=АВ+ВС+АС=2а+2а+а=5а. =>
r=15a:5a=3 (см)
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад