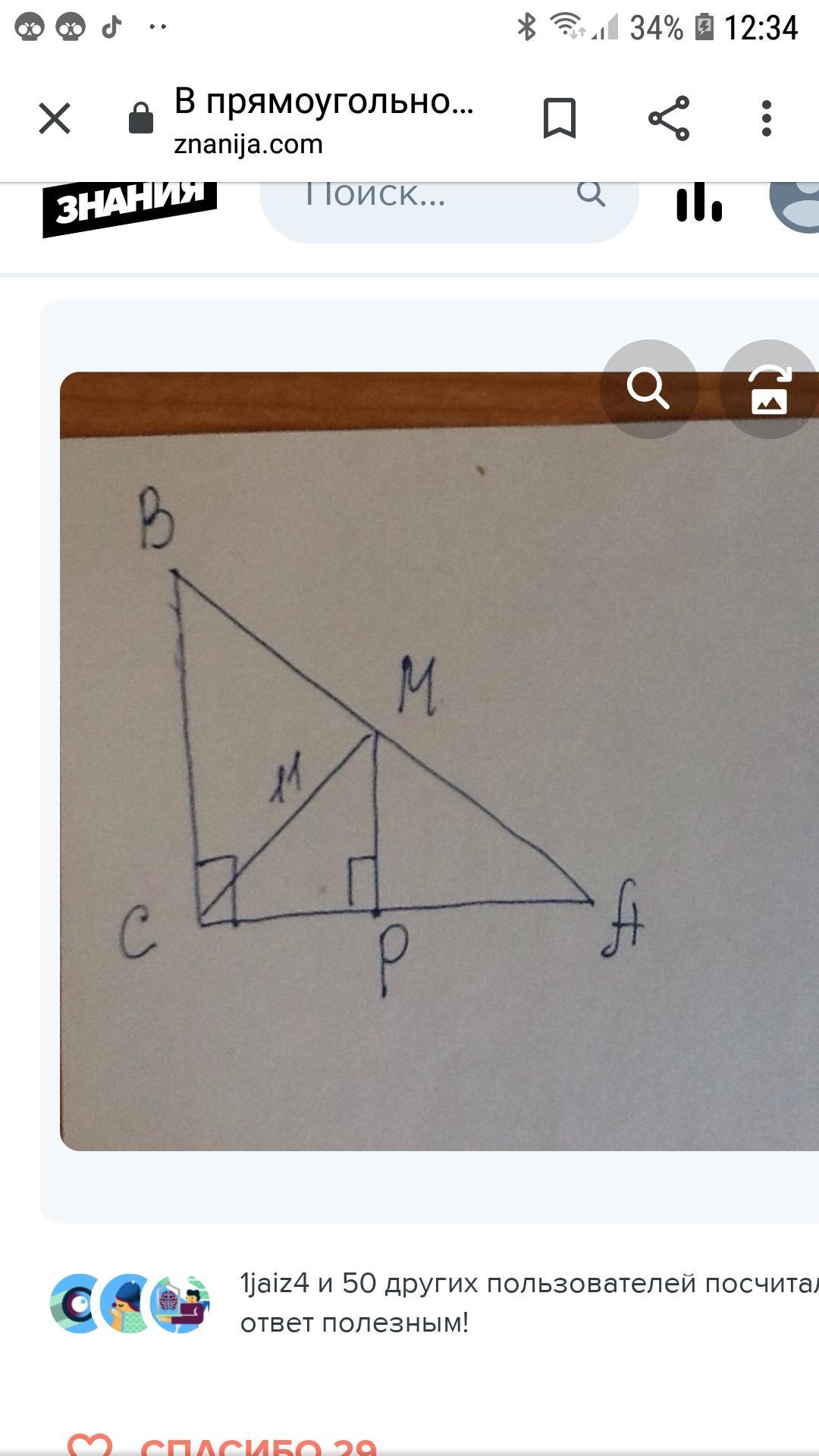
В прямоугольном треугольнике ABC через середину P катета
АС проведён перпендикуляр, пересекающий гипотенузу AB в
точке М. Найдите AB, если СМ = 9 см.
Ответ:
Ответы
Ответ дал:
0
Ответ:СР=РА по условию, МР-перпендикуляр к СА, значит МР║СА и является средней линией ΔАВС. СМ-медиана ΔАВС, т.к. (·) М-середина АВ.
Для медианы прямоугольного треугольника есть формула.
СМ=1/2АВ, значит АВ=2СМ=2*11=22 см
чертеж в файле
Объяснение:
Приложения:
Ответ дал:
0
Ответ:
Объяснение:СР=РА по условию, МР-перпендикуляр к СА, значит МР║СА и является средней линией ΔАВС. СМ-медиана ΔАВС, т.к. (·) М-середина АВ.
Для медианы прямоугольного треугольника есть формула.
СМ=1/2АВ то есть медиана в прямоугольном треугольника опущенная на гипотенузу равна ее половине , значит АВ=2СМ=2*9=18 см
чертеж в файле
Приложения:

Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад