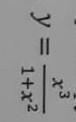Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
экстремумы при помощи первой производной
y'=0 ⇒ x0 = 0 -критическая точка
f(0) = 0
вторая производная
y''(0) = 0 - точка х0= 0 - точка перегиба
ответ
экстремумов нет
Приложения:

Мэри232103:
огромное спасибо!
пожалуйста. обращайтесь -))
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад