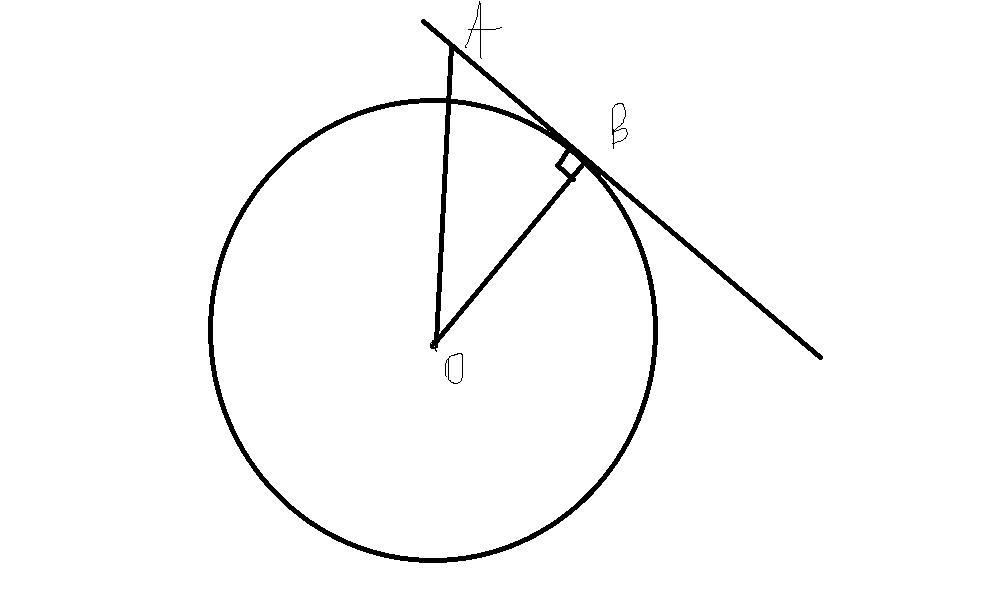
к окружности с центром О проведена касательная AB (B- точка касания). найдите величину угла AOB, если радиус окружности 8 см, OA 16 см
Ответы
Ответ дал:
1
ОВ - радиус окружности, равный 8 см.
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Поэтому треугольник OAB - прямоугольный, ∠ABO = 90°.
OA - гипотенуза, равна 16 см. OB - катет, равен 8 см.
Катет, лежащий против угла 30° равен половине гипотенузы. У нас катет OB равен половине гипотенузы OA, значит ∠OAB = 30°.
По т. о сумме углов треугольника:
∠AOB = 180 - ∠OAB - ∠ABO = 180 - 30 - 90 = 60°
Ответ: 60°
Приложения:
Аноним:
Лучшая!
сану на аве здоровья маме поставишь лучший ;)
Чонгук на аве, здоровье маме)
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад