геометрия помогите решить:Две стороны треугольника равны 7 см и 8 см. Найдите третью сторону треугольника, если она корень из 3 раз больше радиуса окружности, описанной около треугольника. Сколько решений имеет задача?
Приложения:

cos20093:
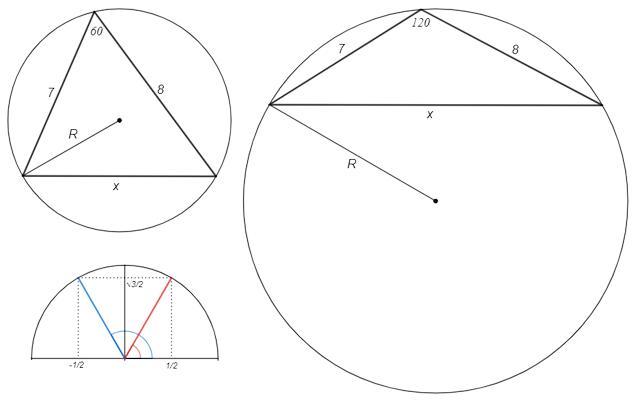
Как всегда, решение очень простое, если зайти "с конца". Есть окружность радиуса R и хорда длины R√3; если эта хорда - сторона вписанного треугольника, то третья вершина должна находиться на окружности. Если она находится с той же стороны от хорды, что и центр, то угол напротив неё 60°, а если с другой - 120°. Дальше надо просто применить теорему косинусов в обоих случаях.
Ответы
Ответ дал:
1
x =R√3 (по условию)
x/sinф =2R (т синусов) => R√3/sinф =2R => sinф =√3/2
0 <ф <180
cosф = +-√(1 -sinф^2) ={-1/2; 1/2}
x^2 =49 +64 -2*56*cosф (т косинусов) =>
1) x =√(113+56) =13 (см)
2) x =√(113-56) =√57 (см)
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад