Решите пожалуйста уравнение
Найти частное решение дифференциального уравнения первого порядка
dy/4x в кубе =dx/y
y(0)=1
Приложения:
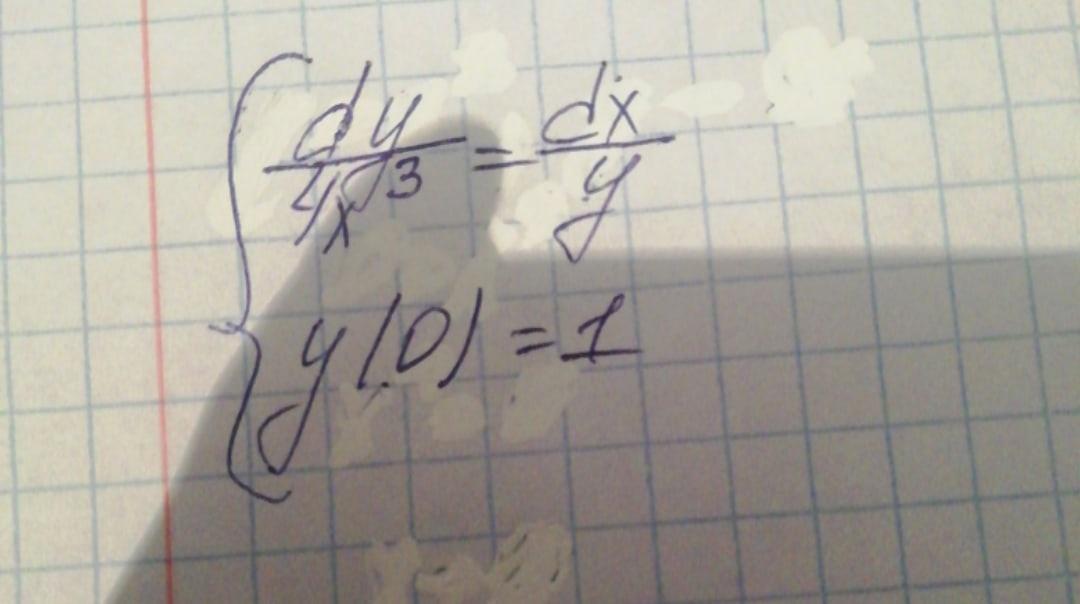
Ответы
Ответ дал:
3
Рассмотрим условие :
Тогда частное решение примет вид:
Аноним:
спс
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад