Решить параметры
Найти решения для всех значение а
lg(x^2 - 3ax) = lg(x - 6a + 2)

Ответы

Ответ дал: Аноним

Ответ:

Объяснение:

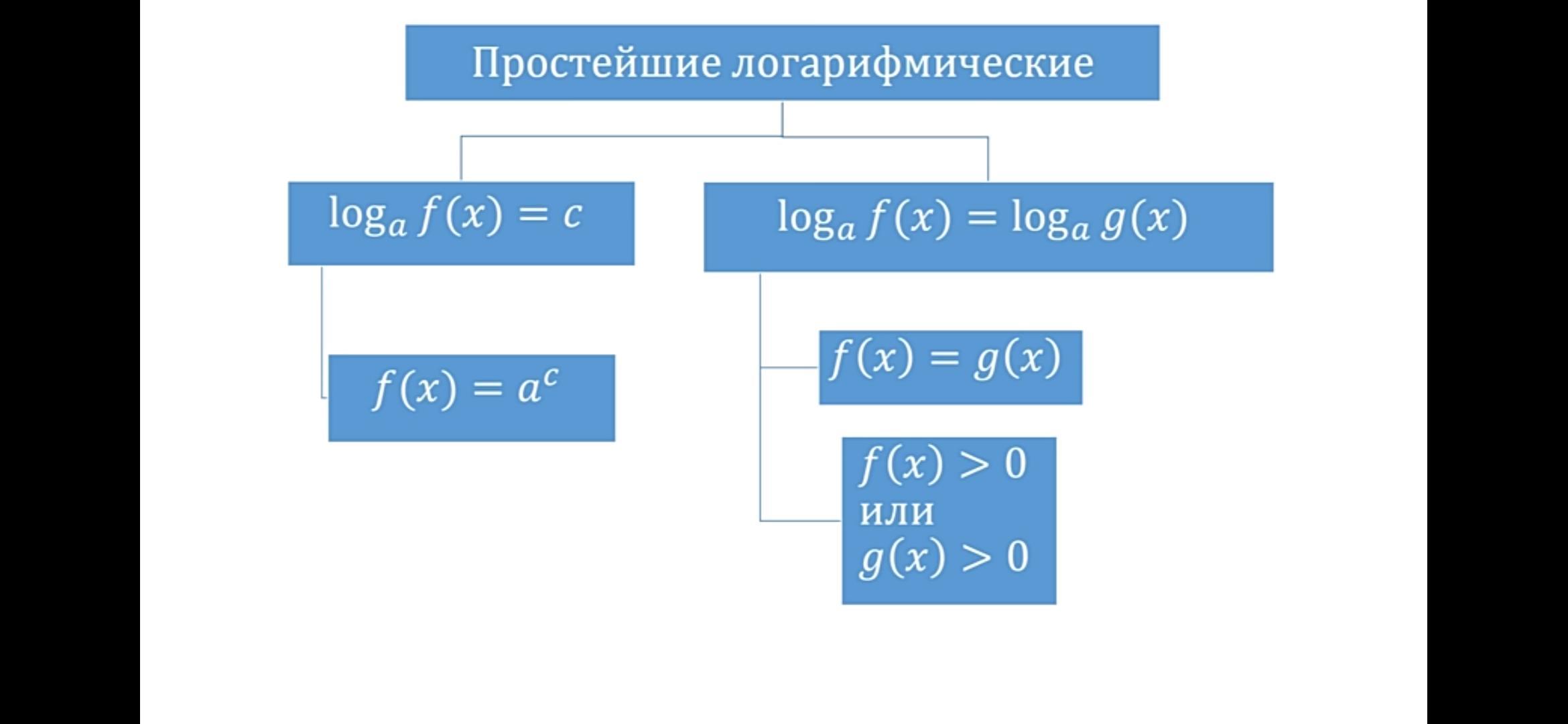
По свойству логарифмов запишем систему: x^2-3ax-x+6a-2 = 0, x - 6a + 2>0

x^2-x(3a+1)+2(3a-1)=0, x>6a-2

(x-2)(x-3a+1)=0, x>6a-2

Подставим каждое значение икс в ОДЗ

2>6a-2

4>6a

a<2/3.

3a-1>6a-2

1>3a

a<1/3 значит итого a<1/3.

Если а < 1/3 то х= 2, х = 3а-1

Если 1/3≤а<2/3 то х=2

Приложения:

Egor761: Спасибо

Egor761: https://znanija.com/task/879264
Посмотри здесь ОДЗ. По твоей схеме не работает

Аноним: Потому что чтобы использовать формулу log[a, b] + log[a, c] = log[a, b*c] необходимо прописать ограничения b>0, c > 0. А потом у тебя сводится к виду log[a, b*c] = log[a, d], где а некоторое положительное число, значит можно не прописывать дополнительные условие и писать сразу b*c = d

Egor761: на счет твоего решения. у меня вопрос, так а ответ конечный вида "если а > ..., то x ..." и т.д. А то не совсем понятно получается, просто a<1/3

Аноним: Поправил ответ

Egor761: если подставить например 2 или 3, все равно ответы получаются такие же. может ты где-то ошибся? . _.

Аноним: Нет, у тебя ошибка где-то.

Egor761: в плане? я подставил вместо а 2 и 3, ответы вышли всё равно. Попробуй

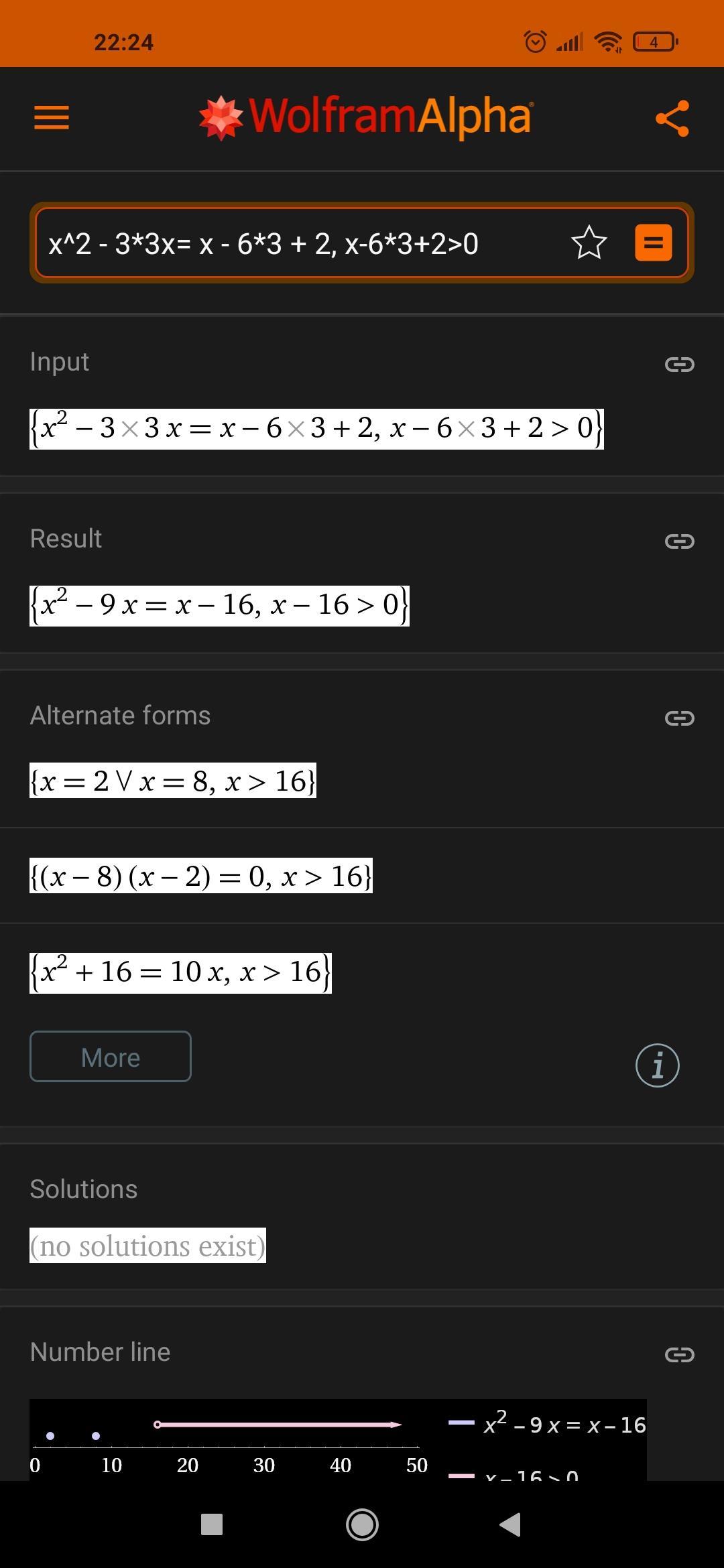
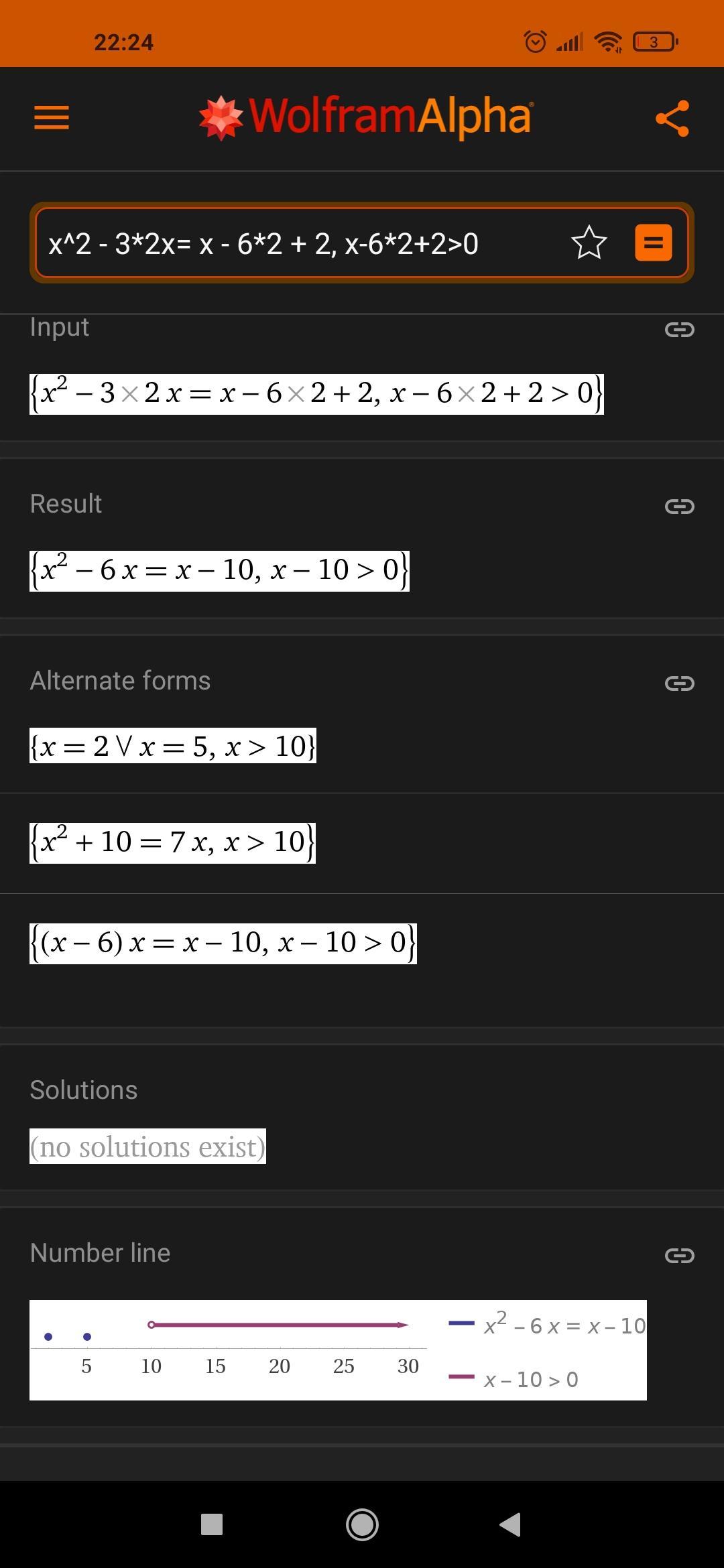
Аноним: Я скинул скрин с вольфрама. Решений нет при х=3, х=2 корень, я тебе сам показал

Аноним: Ой, нет решений при а=3, и при а =2

Вас заинтересует

Английский язык

2 года назад

Переведите пожалуйста в косвенную речь Tom: I'm starting a new school. I worry that I won't have friends here. Sarah: We had long summer holidays. I'm glad that we start learning new things.

Английский язык

2 года назад