Ответы
Ответ дал:
2
Объяснение:
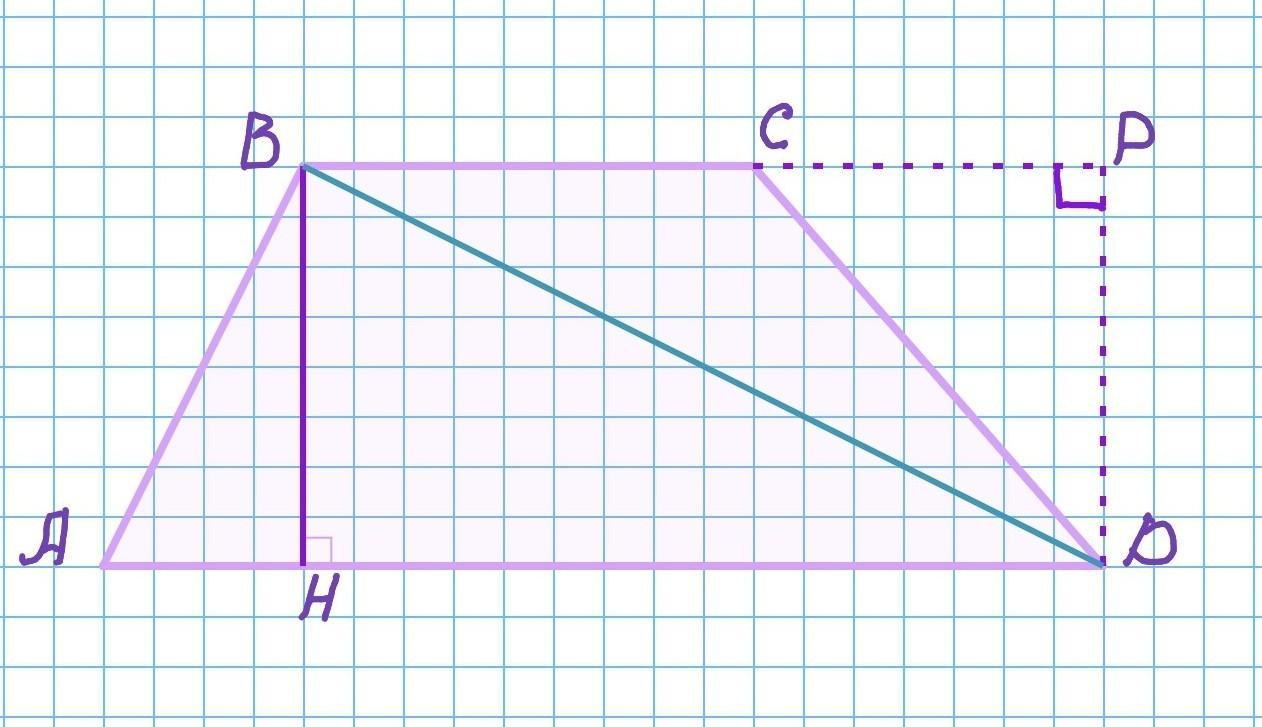
- ТРАПЕЦИЯ это четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.
АВСD - трапеция. ВС II AD. AB и CD - не параллельны.
- Площадь трапеции равна полусумме её оснований, умноженную на высоту.
где BC, AD - основания трапеции, ВН - высота.
Доказательство:
Проведём диагональ BD.
Площадь трапеции равна сумме площадей треугольников АВD и BCD.
Площадь △АВD:
Площадь △BCD:
где PD - внешняя высота тупоугольного треугольника BCD.
Учитывая, что PD=ВН, вынесем за скобки ½•ВН, получаем:
что и требовалось доказать.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад