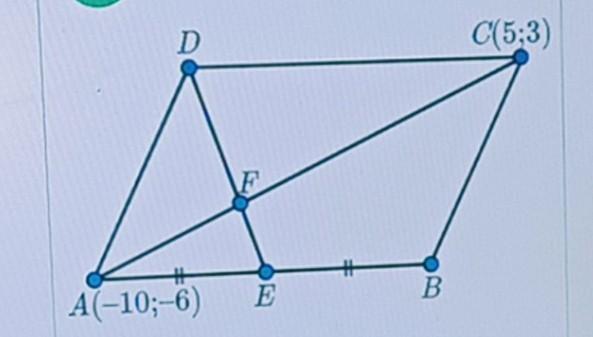
На рисунке ABCD параллелограмм, AE = EB. Найди координаты точки F, если известны координаты точек C(–10; –6) и A(5; 3)
Ответы
Ответ:
F(-5;-3).
Объяснение:
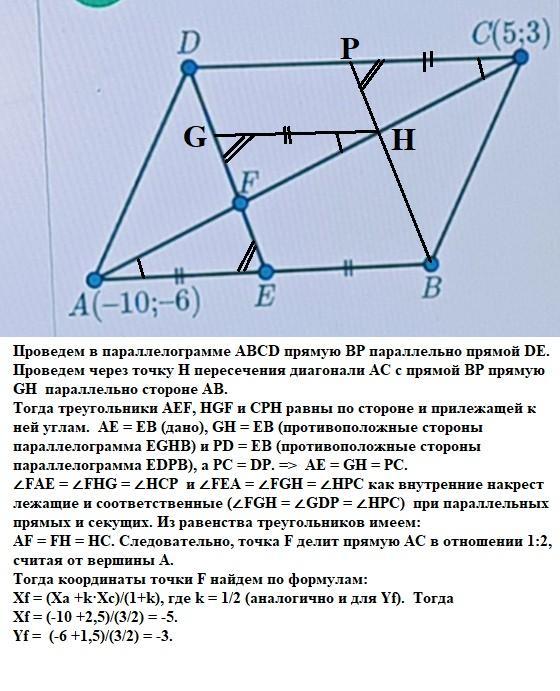
Проведем в параллелограмме АВСD прямую ВР параллельно прямой DE. Проведем через точку Н пересечения диагонали АС с прямой ВР прямую GH параллельно стороне АВ.
Тогда треугольники AEF, HGF и CPH равны по стороне и прилежащей к ней углам. АЕ = ЕВ (дано), GH = EB (противоположные стороны параллелограмма EGHB) и PD = EB (противоположные стороны параллелограмма EDPB), а РС = DР. => AE = GH = PC.
∠FAE = ∠FHG = ∠HCP и ∠FEA = ∠FGH = ∠HPC как внутренние накрест лежащие и соответственные (∠FGH = ∠GDP = ∠HPC) при параллельных прямых и секущих. Из равенства треугольников имеем:
AF = FH = HC. Cледовательно, точка F делит прямую АС в отношении 1:2, считая от вершины А.
Тогда координаты точки F найдем по формулам:
Xf = (Xa +k·Xc)/(1+k), где k = 1/2 (аналогично и для Yf). Тогда
Xf = (-10 +2,5)/(3/2) = -5.
Yf = (-6 +1,5)/(3/2) = -3.