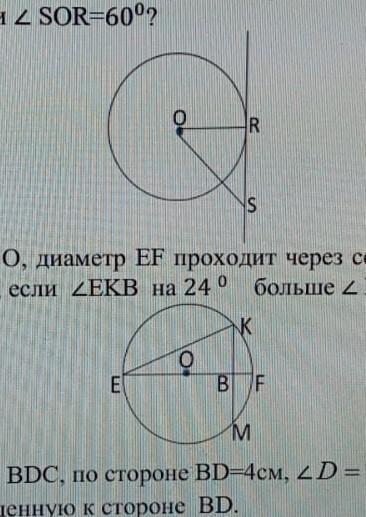
1. прямая SR касается окружности с центром О и радиусом OR=2,3 см, а в точке R. Чему равна отрезка OS, если < SOR=60°
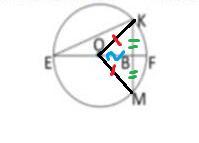
2. В окружности с центром О, диаметр EF проходит через середину хорды KM. Найдите все внутренние углы углЕКВ на 24° больше углВЕК.
3.
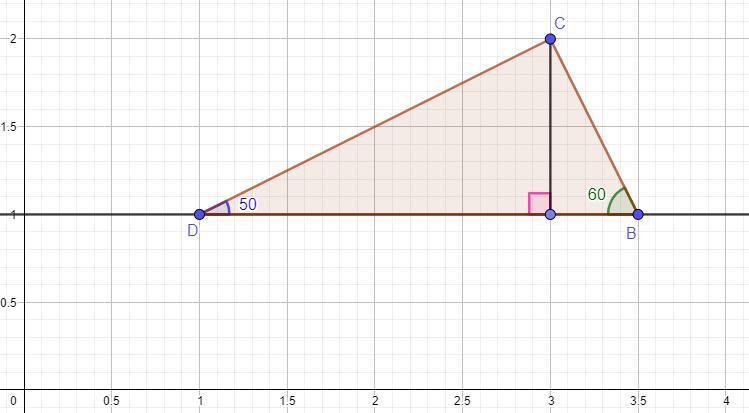
а) Постройте треугольник ВDC, по стороне BD=4см, <D=50°, <В=60°
б) Постройте высоту, преведенную к стороне ВD
Ответы
Ответ:
1. OS = 4,6 см
2.
∠EBK = 90°
∠BEK = 33°
∠EKB = 57°
Объяснение:
1.
Дано: O - центр окружности, OR = 2,3 см, OR ⊥ RS (по свойствам касательной), ∠SOR = 60°
Найти: OS - ?
Решение: Рассмотрим треугольник ΔORS. Так как по условию OR ⊥ RS, то угол ∠ORS = 90°. см.
2.
Дано: O - центр окружности, EF - диаметр, BK = BM, ∠EKB = ∠BEK + 24°
Найти: OS - ?
Решение: Проведем отрезки OK и OM. Так как треугольник ΔKOM - равнобедренный(OK = OM как радиусы), OB - медиана(BK = BM по условию), то по свойствам равнобедренного треугольника медиана проведенная к основанию является биссектрисой и высотой, тогда угол ∠OBK = 90°.
Рассмотрим прямоугольный треугольник ΔBEK. По теореме про сумму углов треугольника: ∠EBK + ∠BKE + ∠KEB = 180°.
∠BEK + 24° + ∠BEK + 90° = 180°.
2∠BEK = 66°|:2
∠BEK = 33°.
∠EKB = ∠BEK + 24° = 33° + 24° = 57°.
3.
Возьмем линейку и проведем отрезок 4 сантиметра. С помощью транспортира построим углы в 50° и 60° и продлим их до пересечения в точки C. Согласно условию обозначим ∠B = 60°, ∠D = 50°. Из точки C проведем перпендикуляр с помощью линейки к стороне BD.