Question

ГЕОМЕТРИЯ ПОЖАЛУЙСТА
ДАЮ ВСЕ БАЛЛЫ
СПАМ- БАН
ПОДРОБНОЕ РЕШЕНИЕ ПОЖАЛУЙСТА ​

Answer 1

Ответ: 30 градусов.

Объяснение:

Радиус, проведенный к точке касания перпендикулярен касательной. Поэтому ОК перпендикулярен NM и треугольник ОMN прямоугольный с прямым углом N. В прямоугольном треугольнике, катет лежащий против угла NMK (ON) равен половине гипотенузы (OM), следовательно угол

NMO равен 30 градусов.

ОК тоже радиус окружности и равен 9. Отрезки касательных из точки М равны (то есть МК=МN. Следовательно угол ОМК = 30 градусов.

Угол NMR = угол NMO+ угол OMK = 30+30 60 градусов

Answer 2

Решение:

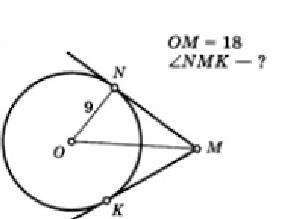
OM = 18, ON = 9. ON - радиус, проведённый к точке касания касательной к окружности, отсюда ∠ONM = 90°. Напротив ∠NMO лежит катет ON, ON = 9, гипотенуза OM = 18, то есть катет ON в два раза меньше гипотенузы OM. Как мы знаем, катет, лежащий напротив угла в 30°, равен половине гипотенузы. Получается, что ∠NMO = 30°. Для ΔOKM аналогичная ситуация (∠OMK = 30°). ∠NMK = ∠NMO + ∠OMK.

∠NMK = 30° + 30° = 60°

Ответ: 60°