Question

Известны три стороны треугольника, равные 5, 6 и 7 см. Найдите
приближённо наименьшую высоту треугольника, считая, что √6‎ равен 2,45.

Answer 1

Відповідь:

4.2

Пояснення:

Еще один вариант

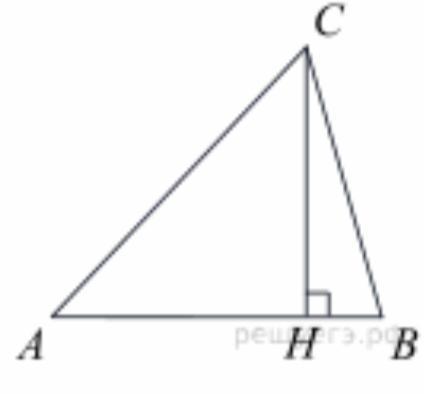
Наименьшая висота будет виходить из наибольшего угла, а напротив наибольшего угла в △ лежит большая сторона.

СВ=5; АВ=7; СА=6

Пусть НВ=х

Тогда АН=7-х

Используя теорему Пифагора для △АСН и △ВСН запишем

СН^2=АС^2-АН^2 и СН^2=ВС^2-ВН^2

АС^2-АН^2 =ВС^2-ВН^2

36-(7-х)^2=25-х^2

36-49+14х-х^2=25-х^2

14х=25+13

х=38/14=19/7

Тогда СН^2=25-(19/7)^2=25-361/49=864/49

СН=√(864/49)=12√6/7=12×2.45/7=4.2

Answer 2

Наименьшая высота в треугольнике проводится к наибольшей стороне, она по условию АВ=7 см

Сторона и высота связаны через площадь треугольника, поэтому вычислю ее по формуле Герона

p=(5+6+7)/2=9

S=√(p(p-a)(p-b)(p-c))=√(9*4*3*2)=6√6

S(ABC)=AB*CH/2

CH=2S/AB=2*6√6/7=12√6/7=12*2.45/7=4.2 cм