Предмет: Математика
Автор: step31121981
Вопрос задан 2 года назад

Прошу помогите мне пожалуйста с одним заданием по МАТЕМАТИКЕ. Зарание спасибо большое Вам Найти промежутки возрастания и убывания функции

Приложения:

amanda2sempl: Производная у' = (2^x - 4^x)' = (ln2) * 2^x - (ln4) * 4^x.
y'=0 then (ln2) * 2^x - (ln4) * 4^x = 0, откуда (ln2) * 2^x = (ln4) * 4^x . Далее (4/2)^x = ln2/ ln4, т.е. 2^x = ln2/ ln4, откуда х = log₂(ln2/ ln4) < 0, так как
0 < ln2/ ln4 < 1

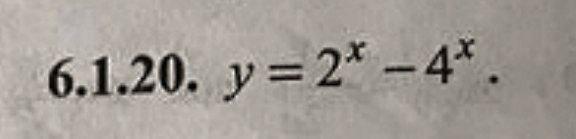
amanda2sempl: Заметим, что ln2/ ln4 = log₄2 = 1/2, значит х = log₂(ln2/ ln4) = log₂(1/2) = -1

amanda2sempl: х = - 1 -точка, где производная обращается в ноль (потенциальная точка экстремума), обратим внимание, что исходная функция определена при любых действительных икс

amanda2sempl: Напомним: у' = (ln2) * 2^x - (ln4) * 4^x - наша производная, расставим ее знаки на числовой оси, разделённую точкой х = - 1 на два интеревала

amanda2sempl: интервала

amanda2sempl: пусть х = 0, правее минус одного, тогда у'(0) = (ln2) * 2^0 - (ln4) * 4^0 = ln2 - ln4 = ln(2/4) = ln(1/2) = - ln2 < 0, значит правее точки х = -1 производная будет всюду отрицательна, а левее точки х = -1 - всюду положительна

amanda2sempl: Промежутки монотонности исходной функции: при х ε (-∞ ; -1 ) функция будет возрастающей, а при х ε (-1 ; +∞ ) - убывающей. Точка х = - 1 - точка максимума

step31121981: Мое Вы золото. Спасибо вам большое за помощь.

amanda2sempl: знаки производной, напоминаем, определяют промежутки возрастания и убывания первоначальной функции

amanda2sempl: ))