Question

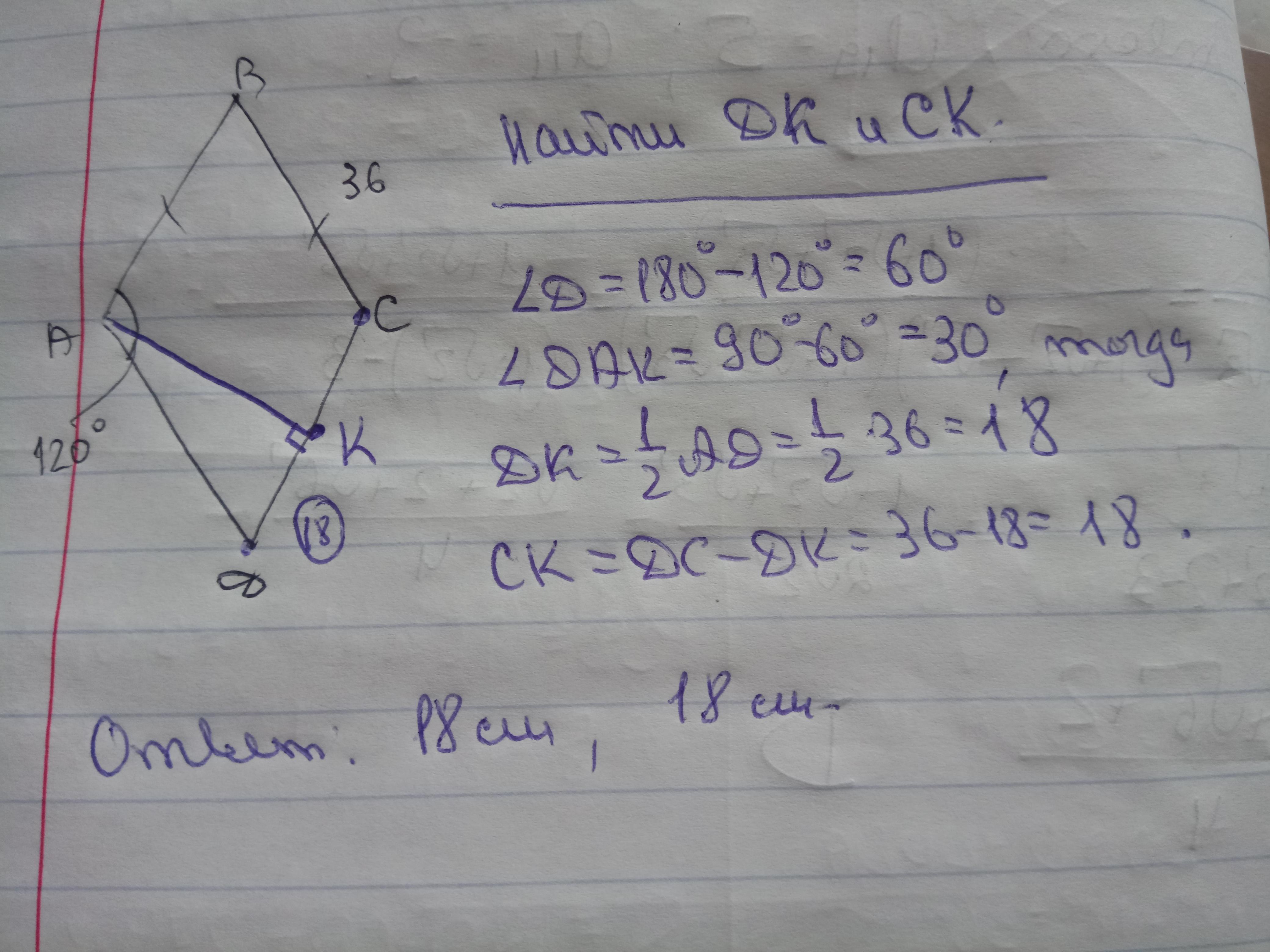
Сторона ромба равна 36, а тупой угол равен
120°. Высота ромба, опущенная из вершины
тупого угла на противоположную сторону, делит
её на два отрезка. Найдите длины этих отрезков.​

Answer 1

18 см, 18 см

Решение задания прилагаю

Answer 2

Ответ:

24.5

Объяснение:

Ромб ABCD

угл А = угл = С = 120°.

360 - 120 - 120 = 120 ÷ 2 = 60

Следует что угл В = угл D = 60° (острые углы).

AH - высота.

Рассмотрим триуг AHB.

угл BAH = 180° - 60° - 90° = 30°.

Отсюда следует что BH = 1/2 BC = 18° т.к. против угла 30° лежит сторона равная половине гипотенузы в прямоугольных треугольниках.