Question

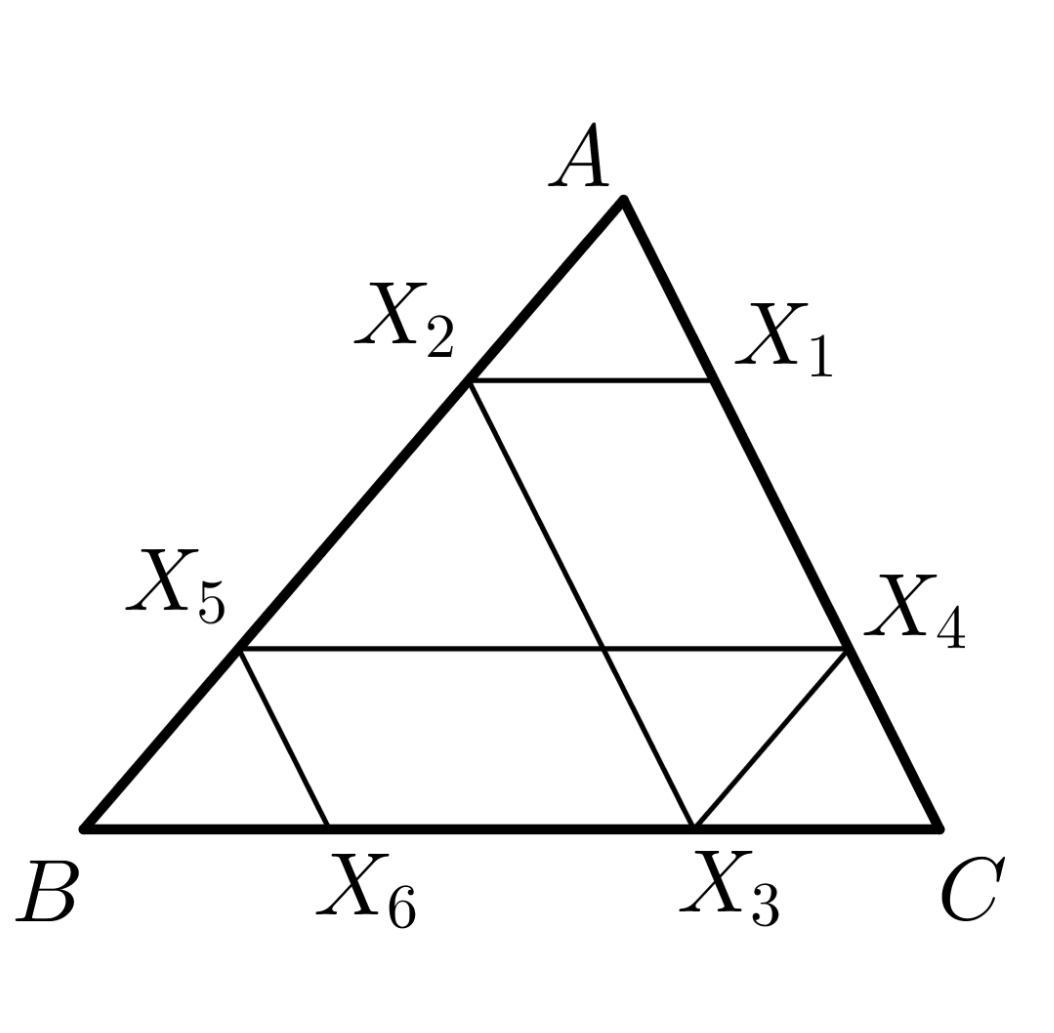
Дан треугольник ABC, в котором AB=12, AC=8, BC=16. На стороне AC выбрана точка X1 такая, что AX1=2. На сторонах треугольника последовательно построены точки X2, X3, X4, X5, X6 такие, что X1X2∥BC, X2X3∥AC, X3X4∥AB, X4X5∥BC, X5X6∥AC. Найдите длину отрезка X3X6.

Answer 1

Ответ:

8

Объяснение: долго расписывать основная мысль такая по теореме фалеса говоришь что AХ1/АХ2=2/3 потом пусть X2X5=2y X1X4=3X далее по аналогии находишь BX5 и с BX6 по фалеса и находишь CX4 CX3 конкретных чисел не помню но BX5=что-то умножить на y и также с  BX6 CX4 CX3(эта штука равна чему-то умножить на y вроде) считаешь углы у параллелограммов которые прям очевидно бросаются в глаза на рисунке дальше говоришь что треугольники AX2X1 И BX5X6 равны ну там поймёшь о чем я посчитав углы, а дальше у тебя будет известны две стороны  на BC и X3X6 легко найдётся. Буду рад если кто-то понял о чем я и напишет более подробное решение.