Question

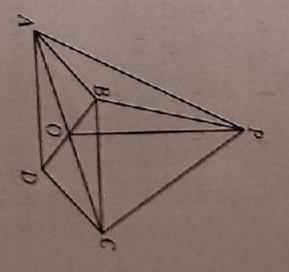
Стороны прямоугольника равны 6 см и 6\/3 см. Кплоскости прямоугольника через точку пересечения его диагоналей проведен перпендикуляр РО, равный 6 см. Найдите угол между прямой РС и плоскостью прямоугольника АВСП.
​

Answer 1

Ответ:

45°

Объяснение:

Дано: РАВСД - пирамида

АВ=а=6,. АД=6√3,. РО=h=6

О-точка пересечения диагоналей

<(PC)(АВСД)=@=?

Решение,. РС-боковое ребро пирамиды,

∆АРС:. АС- диагональ основания,

<РСА=<РСО- искомый угол

АС=√(а^2+В^2)=√((6^2+(6√3)^2)= =√(6^2*(1+3))=12

АС=12

∆РОС - прямоугольный <О=90; ОС=ОА=1/2*АС по условию, (диагонали Прямоугольника точкой пересечения делятся пополам.)

=>. ОС=6,. ОР=6

tg@=OP/OC=6/6=1

@=45°