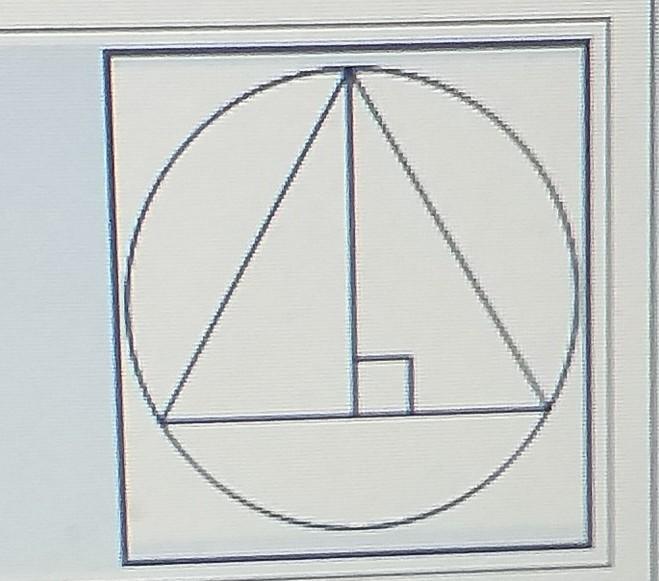
Радиус окружности, описанной около равностороннего треугольника, равен 16. Найдите высоту этого треугольника.
Приложения:
Ответы
Ответ дал:
0
Ответ:
24 см
Объяснение:
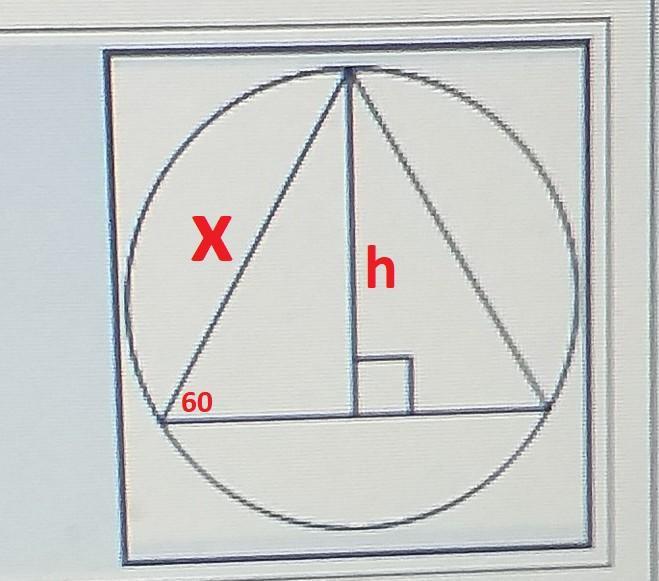
Пусть сторона равностороннего треугольника x, высота h , а радиус описанной окружности R. По свойству правильного треугольника все его углы 60°. По следствию из теоремы синусов:
см.
см.
Смотрите рисунок!!!
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад