Із точок А і С, які лежать в одній півплощині відносно прямої m, опущено перпендикуляри АА1 і СС1 на цю пряму. Відомо, що АА1 = 7 см, СС1=1 см, АС =6 см. Якого найменшого значення може набувати сума АХ + ХС, де Х-точка, що належить прямій m?
siestarjoki:
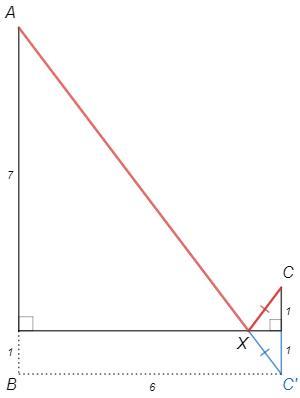
AC' =V(8^2 +6^2) =10
Ответы
Ответ дал:
11
Ответ:
AX+XC =AC' =√(8^2 +6^2) =10
Объяснение:
C' - точка, симметричная С относительно прямой m.
Отрезок AC' - кратчайшее расстояние между точками.
Тогда AX+XC - наименьшая сумма (XC=XC')
Найдем ее как гипотенузу △ABC'
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад