Обчисліть площу трикутника, утвореного осями координат
дотичною до графіка функції f(x) = х2 – 4 у точці з абсцисою
хо = -2.
Ответы
Ответ дал:
4
Відповідь:
1 од²
Пояснення:
треба знайти рівняння дотичної
f'(x)= 2x,
f'(x₀)=2*(-2)= -4( кутовий коефіціент)
f(x₀)=(-2)²-4=0
Підставимо знайдені значення в загальне рівняння дотичної:
у=f'(x₀)(х-x₀)+f(x₀)
у= -4(х-(-2))+0= - 4х+2
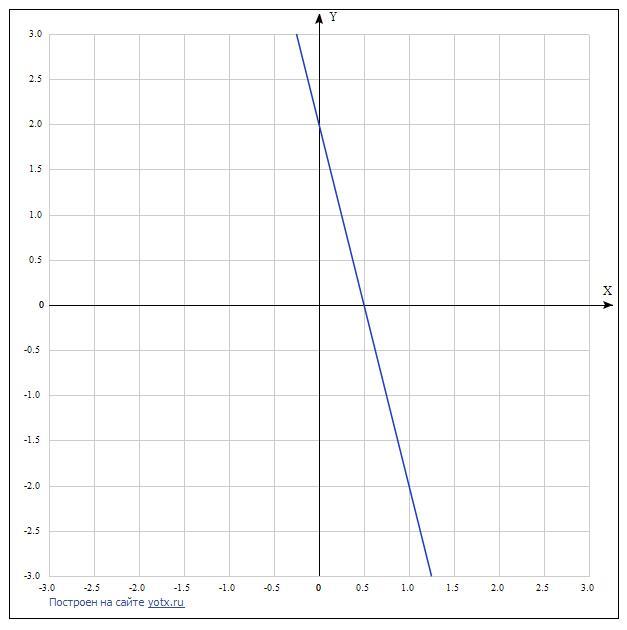
(графік будувати не треба, але щоб було видно Вам трикутник -додаю)
Тепер шукаємо точки перетину з осями координат:
З віссю ОХ :
0= -4х+2;
х=2:4;
х=0,5
З віссю ОУ:
у=-4*0+2;
у=2.
Отже утворився прямокутний трикутник з катетами 2 од. та 0,5 од.
SΔ=1/2 2*0,5=05 од.² ( так як не вказані одиниці: метри, ссантиметри, то ми пишемо од.- одиниці)
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад